AP Board 10th Class Maths Solutions Chapter 10 క్షేత్రమితి Exercise 10.1

SCERT AP 10th Class Maths Textbook Solutions Chapter 10 క్షేత్రమితి Exercise 10.1 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 10th Lesson క్షేత్రమితి Exercise 10.1

ప్రశ్న 1.
క్రమవృత్తాకార శంఖువు ఆకారములో నున్న జోకర్ టోపి యొక్క భూవ్యాసార్ధము 7. సెం.మీ. మరియు ఎత్తు 24 సెం.మీ. ఇటువంటి 10 టోపిలను తయారు చేయడానికి కావలసిన గట్టి అట్టముక్క (షీట్) యొక్క పరిమాణము ఎంత ?
సాధన.

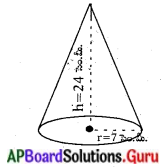
ఇచ్చినవి : శంఖువు ఆకార టోపి ,
వ్యాసార్ధం (r) = 7 సెం.మీ.
ఎత్తు (h) = 24 సెం.మీ.
∴ ఏటవాలు ఎత్తు (l) = [latex]\sqrt{\mathrm{r}^{2}+\mathrm{h}^{2}}[/latex]
= [latex]\sqrt{7^{2}+24^{2}}[/latex]
= [latex]\sqrt{49+576}=\sqrt{625}[/latex]
= 25 సెం.మీ.
∴ ఒక టోపి తయారుచేయుటకు కావలసిన బట్ట యొక్క పరిమాణం = శంఖువు యొక్క ప్రక్కతల వక్రతల వైశాల్యం = πrl
= [latex]\frac{22}{7}[/latex] × 7 × 25 = 550 చ.సెం.మీ.
∴ 10 టోపీలను తయారుచేయుటకు అవసరం అగు బట్ట పరిమాణం = 10 × 550
= 5500 చ.సెం.మీ.

ప్రశ్న 2.
క్రీడా వస్తువులను తయారుచేసే కంపెనీ షటిల్ కాట్లను నిల్వ చేసేందుకు 100 స్థూపాకార కాగితపు డబ్బాలను తయారు చేయాలనుకొంది. స్థూపాకారపు డబ్బా యొక్క కొలతలు 35 సెం.మీ పొడవు/ఎత్తు మరియు భూ వ్యాసార్ధము 7 సెం.మీ ఉండే విధముగా మూతలులేని 100 డబ్బాలను తయారు చేయడానికి కావలసిన కాగితపు పరిమాణము ఎంత ?
సాధన.

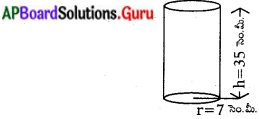
ఇచ్చినవి :
స్థూపాకార కాగితపు డబ్బా వ్యాసార్ధం (r) = 7 సెం.మీ.
ఎత్తు (h) = 35 సెం.మీ.
∴ ఒక స్థూపాకారపు డబ్బా తయారు r = 7 సెం.మీ.
చేయుటకు కావలసిన కాగితపు పరిమాణం = స్థూపం యొక్క సంపూర్ణతల వైశాల్యము = 2πrh
= 2 × [latex]\frac{22}{7}[/latex] × (7) × (35)
= 1540 చ. సెం.మీ.
∴ 100 స్థూపాకారపు డబ్బాలు తయారుచేయుటకు అవసరం అగు కాగితపు పరిమాణం.
= 1540 × 100 = 154000 చ.సెం.మీ.
= [latex]\frac{154000}{100 \times 100}[/latex]
= 15.4 చ|| మీ.

ప్రశ్న 3.
6 సెం.మీ భూవ్యాసార్ధము, 7 సెం.మీ ఎత్తు కల్గిన క్రమ వృత్తాకార శంఖువు యొక్క ఘనపరిమాణమును కనుక్కోండి.
సాధన.

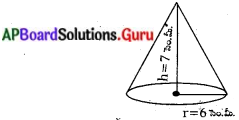
ఇచ్చినవి :
శంఖువు భూవ్యాసార్ధం (r) = 6 సెం.మీ.
శంఖువు యొక్క ఎత్తు (h) = 7 సెం.మీ.
శంఖువు ఘనపరిమాణము = [latex]\frac{1}{3}[/latex] πr²h
= [latex]\frac{1}{3}[/latex] × [latex]\frac{22}{7}[/latex] × 6 × 6 × 7
= 264 ఘ. సెం.మీ.

ప్రశ్న 4.
ఒక స్థూపము యొక్క ఉపరితల వైశాల్యము, శంఖువు యొక్క వక్రతల వైశాల్యమునకు సమానము. రెండింటి యొక్క భూవ్యాసార్ధములు సమానము అయిన స్థూపము యొక్క ఎత్తు, శంఖువు యొక్క ఏటవాలు ఎత్తుల నిష్పత్తి ఎంత ?
సాధన.

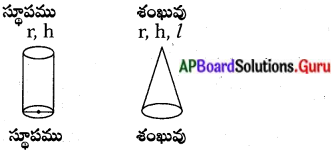
స్థూపము, శంఖువు యొక్క భూవ్యాసార్ధములు సమానము.

CSA/ LSA స్థూపం యొక్క = 2πrh
CSA శంఖువు యొక్క = πrl
స్థూపం యొక్క ఉపరితల వైశాల్యం, శంఖువు యొక్క వక్రతల వైశాల్యానికి సమానం.
2πrh = πrl
[latex]\frac{\mathrm{h}}{l}=\frac{\pi \mathrm{r}}{2 \pi \mathrm{r}}[/latex];
[latex]\frac{\mathrm{h}}{l}=\frac{1}{2}[/latex]
⇒ h : 1 = 1 : 2.

ప్రశ్న 5.
ఒక స్వయం సహాయక బృందం 3 సెం.మీ. భూవ్యాసార్ధం మరియు 4 సెం.మీ ఎత్తు కలి శంఖువు ఆకారములో ఉన్న జోకర్ టోపీలను తయారు చేయాలనుకొంది. వారు 1000 చ.సెం.మీ రంగు కాగితము కలిగి యున్నచో దాని ద్వారా ఎన్ని టోపీలను తయారు చేయగలరు ?
సాధన.

ఇచ్చినవి :
శంఖువు యొక్క వ్యాసార్ధం (r) = 3 సెం.మీ.
ఎత్తు (h) = 4 సెం.మీ.
ఏటవాలు ఎత్తు (l) = [latex]\sqrt{\mathrm{r}^{2}+\mathrm{h}^{2}}[/latex]
= [latex]\sqrt{3^{2}+4^{2}}[/latex]
= 5 సెం.మీ.
శంఖువు ఆకార టోపీ వక్రతల వైశాల్యం = πrl
= [latex]\frac{22}{7}[/latex] × 3 × 5 చ.సెం.మీ.
∴ 1000 చ. సెం.మీ. కలిగిన కాగితం ద్వారా [latex]\frac{22}{7}[/latex] × 3 × 5 చ.సెం.మీ.
వైశాల్యం గల టోపీలను తయారుచేయగల సంఖ్య = [latex]\frac{1000}{\frac{22}{7} \times 3 \times 5}[/latex]
= [latex]\frac{1000 \times 7}{66 \times 5}[/latex]
= 21 . 21 = 21

ప్రశ్న 6.
ఒక స్థూపము మరియు శంఖువు సమాన భూవ్యాసార్ధమును మరియు ఎత్తును కల్గియున్నాయి. అయినచో వాటి ఘనపరిమాణముల నిష్పత్తి 3 : 1 అని చూపుము.
సాధన.
శంఖువు ఘనపరిమాణం (V₁) = [latex]\frac{1}{3}[/latex] π²h
స్థూపం ఘనపరిమాణం (V₂) = πr²h
లెక్క ప్రకారం, స్థూపం మరియు శంఖువు ఘనపరిమాణాల నిష్పత్తి = [latex]\frac{V_{2}}{V_{1}}=\frac{\pi r^{2} h}{\frac{1}{3} \pi r^{2} h}=\frac{1}{\frac{1}{3}}=\frac{3}{1}[/latex] = 3 : 1
∴ V₁ : V₂ = 3 : 1

ప్రశ్న 7.
స్థూపాకారముగా ఉన్న ఇనుప కడ్డీ యొక్క ఎత్తు 11 సెం.మీ. ‘మరియు భూవ్యాసము 7 సెం.మీ. అయినచో ఇటువంటి 50 ఇనుపకడ్డీల యొక్క మొత్తము ఘనపరిమాణము ఎంత ?
సాధన.

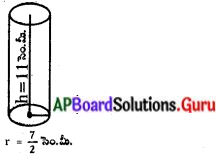
ఇచ్చినవి : స్థూపాకార వ్యాసం (d) = 7 సెం.మీ.
వ్యాసార్థం (r) = [latex]\frac{7}{2}[/latex] సెం.మీ.
ఎత్తు (h) = 11 సెం.మీ.
ఒక స్థూపాకార కడ్డీ ఘనపరిమాణం = πr²h
= [latex]\frac{22}{7}[/latex] × [latex]\frac{7}{2}[/latex] × [latex]\frac{7}{2}[/latex] × 11
= [latex]\frac{22 \times 77}{2 \times 2}=\frac{11 \times 77}{2}[/latex] ఘ. సెం.మీ.
అటువంటి 50 స్థూపాకార కడ్డీల మొత్తం ఘనపరిమాణం (V) = [latex]=\frac{11 \times 77}{2}[/latex] × 50
= 11 × 77 × 25
= 21175 ఘ. సెం.మీ.

ప్రశ్న 8.
ఒక ధాన్యపురాశి 12 మీటర్ల భూవ్యాసము మరియు 8 మీటర్ల ఎత్తు కల్గిన శంఖువు వలే ఉన్నది. అయనచో దాని ఘనపరిమాణము ఎంత ? ఆ ధాన్యపురాశిని కప్పడానికి కావలసిన గుడ్డ పరిమాణము ఎంత ? (π = 3.14 గా తీసుకొనుము)
సాధన.

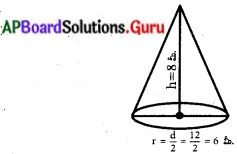
ఇచ్చినవి : శంఖువు ఆకారపు ధాన్యరాశి భూవ్యాసము (d) = 12 మీ.
∴ భూవ్యాసార్ధం = [latex]\frac{\mathrm{d}}{2}=\frac{12}{2}[/latex] = 6 మీ.
శంఖువు ఎత్తు (h) = 8 మీ.
శంఖువాకారపు ధాన్యరాశి ఘనపరిమాణం V = [latex]\frac{1}{3}[/latex] πr²h
= [latex]\frac{1}{3}[/latex] × [latex]\frac{22}{7}[/latex] × 6 × 6 × 8
= 3.14 × 96 = 301.44 మీ³.
ఆ ధాన్యపు రాశిని కప్పడానికి కావలసిన గుడ్డ పరిమాణం = శంఖువు వక్రతల వైశాల్యము = πrl
= [latex]\frac{22}{7}[/latex] × 6 × 10
= 3.14 × 60
= 188.4 చ.మీ.

l = [latex]\sqrt{r^{2}+h^{2}}[/latex]
= [latex]\sqrt{6^{2}+8^{2}}[/latex]
= √100 = 10.

ప్రశ్న 9.
ఒక శంఖువు యొక్క వక్రతల వైశాల్యము . 4070 చ. సెం.మీ. మరియు దాని వ్యాసము 70 సెం.మీ. అయినచో దాని ఏటవాలు ఎత్తును కనుగొనుము.
సాధన.
ఇచ్చినవి : శంఖువు వ్యాసం (d) = 70 సెం.మీ.
వ్యాసార్థం (r) = [latex]\frac{\mathrm{d}}{2}=\frac{70}{2}[/latex] = 35 సెం.మీ.
దాని ఏటవాలు ఎత్తు (l) = ?
శంఖువు వక్రతల వైశాల్యము = 4070 చ.సెం.మీ. లెక్క ప్రకారము, πrl = 4070 సెం.మీ²
[latex]\frac{22}{7}[/latex] × 35 × l = 4070
110 × l = 4070
⇒ l = [latex]\frac{4070}{110}[/latex] = 37 సెం.మీ.
∴ శంఖువు ఏటవాలు ఎత్తు (l) = 37 సెం.మీ.