AP 10th Class Maths Bits 10th Lesson క్షేత్రమితి

Practice the AP 10th Class Maths Bits with Answers 10th Lesson క్షేత్రమితి on a regular basis so that you can attempt exams with utmost confidence.

AP Board 10th Class Maths Bits 10th Lesson క్షేత్రమితి

ప్రశ్న1.
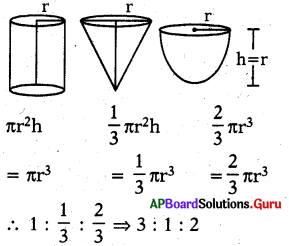
సమాన వ్యాసము మరియు ఎత్తులు గల ఒక శంఖువు మరియు స్థూపం యొక్క ఘనపరిమాణాల నిష్పత్తి ?
జవాబు :
1:3

ప్రశ్న2.
స్థూపం ఘనపరిమాణంనకు సూత్రాన్ని రాయండి.
జవాబు :
πr²h

ప్రశ్న3.
శంఖువు ఘనపరిమాణం కనుగొనుటకు ఉపయోగించే సూత్రాన్ని రాయండి.
జవాబు :
[latex]\frac{1}{3}[/latex]πr²h

ప్రశ్న4.
గోళము, స్థూపము, శంఖువు ఒకే ఎత్తు, ఒకే వ్యాసార్ధాన్ని కలిగి ఉంటే వాటి వక్రతల వైశాల్యాల నిష్పత్తి ఎంత ?
జవాబు :
4: 4: √5

ప్రశ్న5.
ఘనం సంపూర్ణతల వైశాల్యము 54 సెం.మీ.2 అయిన దాని భుజం పొడవు ఎంత ?
జవాబు :
6a² = 54 ⇒ a² = [latex]\frac{54}{6}[/latex] = 9 సెం.మీ.
a = √9 = 3 సెం.మీ.

ప్రశ్న6.
క్రమ వృత్తాకార స్థూప భూ వైశాల్యం 154 సెం.మీ2 అయిన దాని వ్యాసార్ధం ఎంత ?
జవాబు :
πr² = 154
⇒ r² = 154 × [latex]\frac{7}{22}[/latex] = 7 × 7
⇒ r² = 7²
∴ r = 7 సెం.మీ.

ప్రశ్న7.
ఒక శంఖువు వ్యాసం మరియు ఎత్తు 8 సెం.మీ. మరియు 3 సెం.మీ. అయిన దాని ఏటవాలు ఎత్తును కనుగొనుము.
జవాబు :
ఏటవాలు ఎత్తు l = [latex]\sqrt{r^{2}+h^{2}}[/latex]
[latex]\sqrt{4^{2}+3^{2}}[/latex] = 5 సెం.మీ.
(∵ d = 8 ⇒ r = 4)

ప్రశ్న8.
వ్యాసార్ధం r గా గల అర్ధగోళ ఉపరితల వైశాల్యము ఎంత ?
జవాబు :
3πr²

ప్రశ్న9.
1 సెం.మీ. భుజంగా గల ఘనం యొక్క ఘనపరిమాణం ఎంత ?
జవాబు :
1 ఘ. సెం.మీ. (లేదా) 1 సెం.మీ.³

ప్రశ్న10.
రెండు గోళాల ఘనపరిమాణాల నిష్పత్తి 8:27 అయిన వాటి వక్రతల వైశాల్యాల నిష్పత్తి ఎంత ?
జవాబు :
4:9

ప్రశ్న11.
‘ఫుట్ బాల్’ ఏ జ్యా మితీయ నమూనా ?
జవాబు :
గోళం

ప్రశ్న12.
శంఖువు వ్యాసార్ధం (r), ఎత్తు (h), ఏటవాలు (l) అయిన ఈ క్రింది వాటిలో ఏది అసత్యం ?
A) ఎల్లప్పుడు l > h
B) ఎల్లప్పుడు l >r
C) ఎల్లప్పుడు r > l
D) l² = r² + h²
జవాబు :
C) ఎల్లప్పుడు r > l

ప్రశ్న13.
ఒక శంఖువు భూ వ్యాసార్ధం (r), ఎత్తు (h), వాలు ఎత్తు (l), అయిన ‘l’ విలువ ‘r’ మరియు ‘h’ పదాలలో తెల్పండి.
జవాబు :
l = [latex]\sqrt{\mathrm{r}^{2}+\mathrm{h}^{2}}[/latex]

ప్రశ్న14.
రెండు గోళాల ఘనపరిమాణముల నిష్పత్తి 8 : 27 అయితే వాటి వక్రతల వైశాల్యముల మధ్యగల నిష్పత్తి ఎంత ?
జవాబు :
4:9

ప్రశ్న15.
‘α’ భుజము కలిగిన ఒక సమఘనాకార పెట్టెలో పూర్తిగా అమరగలిగిన ఒక ఘనాకృతిలో గల బంతిని ఉంచితే, ఆ బంతి యొక్క ఘనపరిమాణము ఎంత ?
జవాబు :
r = [latex]\frac{α}{2}[/latex]
∴ బంతి ఘనపరిమాణం = [latex]\sqrt{r^{2}+h^{2}}[/latex]πr³
= [latex]\sqrt{r^{2}+h^{2}}[/latex]π[latex]\left(\frac{\alpha}{2}\right)^{3}[/latex] = [latex]\frac{1}{6}[/latex]πα³

ప్రశ్న16.
పట్టకం యొక్క భూవైశాల్యం 30 చ.సెం.మీ. మరియు ఎత్తు 10 సెం.మీ. అయిన పట్టకము ఘనపరిమాణంను కనుగొనుము.
జవాబు :
పట్టకం ఘనపరిమాణం = భూవైశాల్యం × ఎత్తు
= 30 × 10 = 300 ఘ. సెం.మీ.

ప్రశ్న17.
ఘనము యొక్క సంపూర్ణతల వైశాల్యము 96 ఘ. సెం.మీ. అయిన ఆ ఘనము యొక్క భుజం ఎంత?
జవాబు :
6a² = 96 ⇒ a² = 16
∴ a = [latex]\sqrt{16}[/latex] = 4 సెం.మీ.

ప్రశ్న18.
ఒక క్రమ వృత్తాకార స్థూపము యొక్క వ్యాసార్ధం 6 సెం.మీ., ఎత్తు 1 సెం.మీ., అయిన దాని ఘనపరిమాణమును కనుగొనుము.
జవాబు :
r = 6, h = 7
స్థూపం ఘనపరిమాణం V = πr²h
= [latex]\frac{22}{7}[/latex] × (6)² × 7 = 22 × 36
= 792 ఘ. సెం.మీ.

ప్రశ్న19.
‘r’ వ్యాసార్ధం గల ఒక గోళం, స్థూపంలో, సరిగ్గా అమరింది. గోళం ఉపరితల వైశాల్యం స్థూపం యొక్క ……………. కు సమానం
A) సంపూర్ణతల వైశాల్యం
B) వక్రతల వైశాల్యం
C) ఘనపరిమాణం
D) ఏదీకాదు
జవాబు :
B) వక్రతల వైశాల్యం

ప్రశ్న20.
10 సెం.మీ. వ్యాసార్ధం గల గోళ వక్రతల వైశాల్యంను πలలో తెల్పండి.
జవాబు :
గోళం వక్రతల వైశాల్యం = 4πr²
= 4π(10²) = 400 π చ. సెం.మీ.

ప్రశ్న21.
ఒక సమ ఘనం యొక్క సంపూర్ణతల వైశాల్యం 216 సెం.మీ.2 అయిన దాని ఘనపరిమాణము ఎంత?
జవాబు :
6a² = 216 ⇒ a² = 36.
⇒ a = [latex]\sqrt{36}[/latex] = 6 సెం.మీ.
∴ ఘనపరిమాణం V = a³ = 6³ = 216 ఘ. సెం.మీ.

ప్రశ్న22.
ప్రాచీన భారత గణిత శాస్త్రవేత్త ఆర్యభట్ట యొక్క ప్రసిద్ధ గ్రంథం
A) ఆర్య తర్కం
B) ఆర్య భట్టీయం
C) సిద్ధాంత శిరోమణి
D) కరణ కుతూహలం
జవాబు :
B) ఆర్య భట్టీయం

ప్రశ్న23.
క్రింది A, B పాత్రలలో ఏ పాత్రలో ఎక్కువ నీటిని నింపవచ్చును ? (A, Bలు స్థూపాకారంలో కలవు)

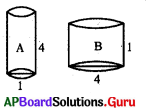
A) A
B) B
C) A, Bలలో సమాన పరిమాణంలో నీటిని నింపవచ్చును.
D) నిర్ణయించలేము
జవాబు :
B) B

ప్రశ్న24.
8 × 4 × 1 కొలతలు గల దీర్ఘఘనంలో ఉంచగల అతి పెద్ద కర్ర పొడవు ఎంత ?
జవాబు :
అతి పెద్ద కర్ర పొడవు = [latex]\sqrt{l^{2}+b^{2}+h^{2}}[/latex]
= [latex]\sqrt{8^{2}+4^{2}+1^{2}}=\sqrt{64+16+1}=\sqrt{81}[/latex]
= 9 యూనిట్లు

ప్రశ్న25.
ఒక స్థూపము మరియు శంఖువు సమాన భూవ్యాసార్ధమును మరియు ఎత్తును కల్గియున్నాయి. అయినచో వాటి ఘనపరిమాణాల నిష్పత్తి ఎంత ?
జవాబు :
3:1

ప్రశ్న26.
7 సెం.మీ. వ్యాసార్ధం గల ఘన అర్ధగోళం సంపూర్ణతల వైశాల్యంను కనుగొనుము.
జవాబు :
r = 7, అర్ధగోళ సంపూర్ణతల వైశాల్యం = 3πr²
= 3 × [latex]\frac{22}{7}[/latex] × 7 × 7.
= 3 × 22 × 7 = 462 చ.సెం.మీ.

ప్రశ్న27.
ఒక ఘనం సంపూర్ణతల వైశాల్యం 96 చ.సెం.మీ. అయిన దాని ఘనపరిమాణం ఎంత ?
జవాబు :
6a² = 96 ⇒ a² = 16 ⇒ a = 4
∴ ఘనం ఘనపరిమాణం V = a³
= 4³ = 64 ఘ. సెం.మీ.

ప్రశ్న28.
3 సెం.మీ. వ్యాసార్ధము మరియు 8 సెం.మీ. ఎత్తు కలిగిన శంఖువు ఘనపరిమాణంను π లో తెల్పండి.
జవాబు :
r = 3, h = 8,
శంఖువు ఘనపరిమాణం = [latex]\frac{1}{3}[/latex]πr²h
= [latex]\frac{1}{3}[/latex] π(3)² × 8 = 24 π ఘ. సెం.మీ.

ప్రశ్న29.
ఒకే వ్యాసార్థం, ఎత్తు గల ఒక స్థూపము మరియు ఒక శంఖువు కలవు. స్థూపము యొక్క ఘనపరిమాణం 27 ఘనపు యూనిట్లు అయిన శంఖువు ఘనపరిమాణం ఎంత ?
జవాబు :
శంఖువు ఘనపరిమాణం = [latex]\frac{1}{3}[/latex] స్థూపం ఘనపరిమాణం
= [latex]\frac{1}{3}[/latex] × 27 = 9 ఘ.యూనిట్లు.

ప్రశ్న30.
షేడ్ చేసిన ప్రాంత వైశాల్యం

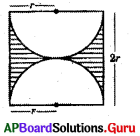
A) r² (2 – π)
B) r² (4 – π)
C) r² (5 – π)
D) r² (6 – π)
జవాబు :
B) r² (4 – π)

ప్రశ్న31.
7 సెం.మీ. వ్యాసార్ధంగా గల అర్ధగోళ సంపూర్ణతల వైశాల్యంను π లో తెల్పండి.
జవాబు :
r = 7 సెం.మీ., . అర్ధగోళ సంపూర్ణతల వైశాల్యం = 3πr²
= 3π(7)² = 147 π చ. సెం.మీ.

ప్రశ్న32.
16 సెం.మీ. వ్యాసం, 15 సెం.మీ.లు ఎత్తు గల శంఖువు యొక్క ప్రక్కతల వైశాల్యంను π లో తెల్పండి.
జవాబు :
d = 16 ⇒ r = 8, h = 15.
∴ l = [latex]\sqrt{r^{2}+h^{2}}=\sqrt{8^{2}+15^{2}}[/latex]
= [latex]\sqrt{64+225}=\sqrt{289}[/latex] = 17

శంఖువు ప్రక్కతల వైశాల్యం = πrl
= π(8) (17) = 136 π చ.సెం.మీ.

ప్రశ్న33.
వ్యాసార్థం r, ఎత్తు యూనిట్లుగా గల శంఖువు ఆకార ప్లాస్కునిండా నీరు కలదు. m వ్యాసార్ధం గల స్థూపాకార ప్లాస్కులో నీటిని నింపగా ఆ నీటి మట్టం ఎత్తును h, π లలో తెల్పండి.
జవాబు :
స్థూపం ఘనపరిమాణం = శంఖువు ఘనపరిమాణం

నీటి మట్టం ఎత్తు h₁ = [latex]\frac{r^{2} h}{3 m^{2}}[/latex]

ప్రశ్న34.
రెండు గోళాల ఉపరితల వైశాల్యాల నిష్పత్తి 1 : 4 అయిన వాని ఘనపరిమాణాల నిష్పత్తి ఎంత ?
జవాబు :
4πr₁² : 4πr₁² = 1 : 4
⇒ r₁² : r₂² ⇒ r₁ : r₂ = 1 : 2
V₁ : V₂ = [latex]\frac{4}{3}[/latex]πr₁³ : [latex]\frac{4}{3}[/latex]πr₂³ = r₁³ : r₂³
= 1³ : 2³ = 1:8

ప్రశ్న35.
4.2 సెం.మీ. భుజంగా గల ఒక సమఘనం నుండి తయారుచేయగల అతి పెద్ద శంఖువు యొక్క ఘనపరిమాణం ఎంత ?
జవాబు :
శంఖువు ఎత్తు = భూవ్యాసం = ఘనం భుజం = 4.2
h = 4.2, r = [latex]\frac{4.2}{2}[/latex] = 2.1

ప్రశ్న36.
6 సెం.మీ.లు వ్యాసంగా గల ఒక లోహపు గోళాన్ని 2 సెం.మీ.లు. వ్యాసంగా గల ఒక సన్నని తీగగా మార్చగా దాని పొడవు ఎంత ?
జవాబు :
గోళం ఘనపరిమాణం = తీగ ఘనపరిమాణం

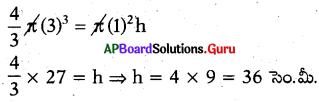
ప్రశ్న37.
‘r’ వ్యాసార్ధంగా గల ఒక లోహపు గోళాన్ని ‘r” యూనిట్లు ఎత్తు గల ఒక లోహపు శంఖువుగా మలిస్తే దాని వ్యాసార్ధం, గోళ్ల వ్యాసార్ధమునకు ఎన్ని రెట్లు ఉంటుంది ?
జవాబు :
[latex]\frac{4}{3}[/latex]πr₂³ = [latex]\frac{1}{3}[/latex]πr₂²(r₁) (శంఖువు ఎత్తు h = r₁ r₂ – శంఖువు వ్యాసార్ధం )
4r₁³ = r₂²r₁² =4r₁² = r₂ ⇒ r₂ = r₂ = [latex]\sqrt{4 r_{1}^{2}}[/latex] = 2r₁ శంఖువు వ్యాసార్ధం, గోళం వ్యాసార్ధానికి 2 రెట్లు ఉంటుంది.

ప్రశ్న38.
49 × 33 × 24 సెం.మీ.లు కొలతలు గల ఒక దీర్ఘఘనాన్ని ఒక గోళంగా మలిస్తే దాని వ్యాసార్థం విలువ ఎంత?
జవాబు :
గోళం ఘనపరిమాణం = దీర్ఘఘనం ఘనపరిమాణం

ప్రశ్న39.
ఒక శంఖువు యొక్క వ్యాసార్థం r, ఎత్తు h, ఏటవాలు ఎత్తు = l అయిన క్రింది వానిలో ఏది సత్యం ?
A) l² = r² + h²
B) l² > r² + h²
C) l² < r² + h²
D) l = r + h
జవాబు :
A) l² = r² + h²

ప్రశ్న40.
8 సెం.మీ.లు వ్యాసార్ధం. గల ఒక గోళం నుండి 1 సెం.మీ. వ్యాసార్ధం గల బంతులు ఎన్ని తయారు చేయగలం ?
జవాబు :

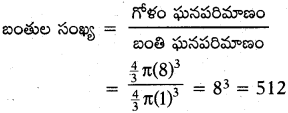
ప్రశ్న41.
శంఖువు వక్రతల వైశాల్యం πrl లో ‘l’ దేనిని సూచిస్తుంది / దేనికి ప్రాతినిథ్యం వహిస్తుంది ?
జవాబు :
ఏటవాలు ఎత్తు

ప్రశ్న42.
రెండు శంఖువుల ఘనపరిమాణాల . నిష్పత్తి 4 : 5 మరియు వాని వ్యాసార్ధాల నిష్పత్తి 2 : 3. వాని ఎత్తుల నిష్పత్తి ఎంత ?
జవాబు :

ప్రశ్న43.
సమాన భూ వ్యాసార్ధాలు వ్యాసార్ధానికి సమాన ఎత్తు గల ఒక శంఖువు మరియు అర్ధగోళం యొక్క ఘనపరిమాణాల నిష్పత్తిని తెల్పండి.
జవాబు :
శంఖువు ఘనపరిమాణం = అర్ధగోళ ఘనపరిమాణం

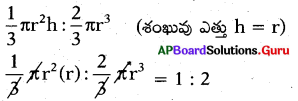
ప్రశ్న44.
స్థూపాకార పాత్ర ఘనపరిమాణం, 448 π సెం.మీ 3, దాని ఎత్తు 7 సెం.మీ. అయిన దాని వ్యాసార్ధం ఎంత?
జవాబు :

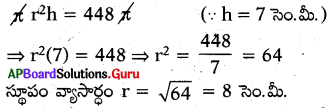
ప్రశ్న45.
14 సెం.మీ.లు భుజంగా గల ఒక సమఘనంలో ఏర్పరచగల (అమర్చగల) అతి పెద్ద స్థూపాకారం యొక్క ఘనపరిమాణంను లెక్కించండి.
జవాబు :
స్థూపం భూవ్యాసం = సమఘనం యొక్క భుజం
స్థూపం భూవ్యాసం d = 14 సెం.మీ.
∴ స్థూపం వ్యాసార్ధం r = 7 సెం.మీ.,
ఎత్తు h = 14 సెం.మీ. .

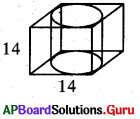
∴ అతి పెద్ద స్థూపం ఘనపరిమాణం = πr²h
= [latex]\frac{22}{7}[/latex] × 7² × 14.
= 22 × 7 × 14 = 2,156 ఘ. సెం.మీ.

ప్రశ్న46.
షటిల్ కాక్ ఈ క్రింది రెండు ఆకారాల సమ్మేళనం.
A) స్థూపం, గోళం
B) గోళం, శంఖువు
C) స్థూపం, అర్ధగోళం
D) అర్ధగోళం, అర్ధశంఖువు
జవాబు :
D) అర్ధగోళం, అర్ధశంఖువు

ప్రశ్న47.
ప్రవచనం-A : సమాన . భూవ్యాసార్ధము మరియు ఎత్తును కలిగిన స్థూపం మరియు శంఖువుల ఘనపరిమాణాల నిష్పత్తి 1 : 3.
ప్రవచనం-B : ఒక అర్ధగోళం యొక్క వక్రతల మరియు సంపూర్ణతల వైశాల్యాల నిష్పత్తి 2 : 3.
A) A – సత్యం, P – అసత్యం
B) A – అసత్యం, B – సత్యం
C) A, B లు రెండూ సత్యం
D) A, B లు రెండూ అసత్యం
జవాబు :
A) A – సత్యం, P – అసత్యం

ప్రశ్న48.
ఒక స్థూపం యొక్క వ్యాసార్ధాన్ని రెట్టింపు చేసి దాని ఎత్తును మార్చకుండా ఉంటే దాని ప్రక్కతల వైశాల్యంలో పెరుగుదల ఎన్ని రెట్లు ఉంటుంది ?
జవాబు :
స్థూపం ప్రక్కతల వైశాల్యం = 2πrh
r₁ → 2r, h₁ → h.
వ్యాసార్ధం రెట్టింపు అయిన తరువాత స్థూపం ప్రక్కతల వైశాల్యం = 2π(2r)h = 4πrh
∴ పెరుగుదల = 4πrh – 2πrh
= 2πrh చ.సెం.మీ.

ప్రశ్న49.
6 సెం.మీ. భుజంగా గల ఒక సమఘనం నుండి 2 సెం.మీ.లు భుజం గల సమఘనాలు ఎన్ని తయారు చేయగలం ?
జవాబు :
తయారు చేయగల సమఘనాల సంఖ్య

ప్రశ్న50.
ఒక గోళం యొక్క ఘనపరిమాణము మరియు ఉపరితలం వైశాల్యాలు సంఖ్యాపరంగా సమానాలు. ఆ గోళం వ్యాసార్ధంను కనుగొనుము.
జవాబు :
[latex]\frac{4}{3}[/latex]πr³ = 4πr² ⇒ r = 3
∴ గోళం వ్యాసార్ధం = 3 యూనిట్లు

ప్రశ్న51.
వ్యాసం ‘d’ గా గల ఒక గోళం యొక్క ఘనపరిమాణంను dలో తెల్పండి.
జవాబు :
గోళం ఘనపరిమాణం = [latex]\frac{4}{3}[/latex]πr³
= [latex]\frac{4}{3}[/latex]π[latex]\left(\frac{d}{2}\right)^{3}=\frac{1}{6}[/latex] πd³

ప్రశ్న52.
రెండు గోళాల వ్యాసార్ధాల నిష్పత్తి 2 : 3 అయిన వాని . ఉపరితల వైశాల్యాల నిష్పత్తి ఎంత ?
జవాబు :
రెండు గోళాల వ్యాసార్ధాల నిష్పత్తి = 2:3
వాని ఉపరితల వైశాల్యాల నిష్పత్తి = 2² : 3²
= 4:9

ప్రశ్న53.
‘r’ వ్యాసార్ధంగా గల ఒక అర్ధగోళంలో అమర్చగల అతిపెద్ద శంఖువు యొక్క ఘనపరిమాణం ఎంత ?
జవాబు :

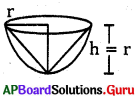
శంఖువు వ్యాసార్ధం r = r, ఎత్తు h = r
∴ శంఖువు ఘనపరిమాణం = [latex]\frac{1}{3}[/latex]π²h
[latex]\frac{1}{3}[/latex]π²(r) = [latex]\frac{1}{3}[/latex]π³ ఘ. యూనిట్లు

ప్రశ్న54.
ఒక స్థూపం, శంఖువు మరియు అర్ధగోళాలు ఒకే భూవ్యాసార్ధం మరియు ఎత్తులు కల్గి ఉన్నచో వాని ఘనపరిమాణాల నిష్పత్తిని రాయండి.
A) 3 : 1 : 2
B) 3 : 2 : 1
C) 1 : 2 : 3
D) 1 : 3 : 2
జవాబు :
A) 3 : 1 : 2

ప్రశ్న55.

పై పటంలో వాడిగా చెక్క పెన్ను చూపడం జరిగినది. ఈ ఘనాకృతిలో గల త్రిమితీయ ఆకారాల పేర్లను తెల్పండి / పై పటం ఏఏ ఘనాకృతల సమ్మేళనము ?
జవాబు :
అర్ధగోళము, స్థూపము, శంఖువు.

ప్రశ్న56.
ఒక స్థూపం యొక్క ఎత్తును రెట్టింపు చేసి దాని వ్యాసార్ధాన్ని 3 రెట్లు చేసిన దాని ఉపరితల వైశాల్యం మొదటి స్థూపం ఉపరితల వైశాల్యమునకు ఎన్ని రెట్లు?
జవాబు :
మొదటి స్థూపం ఉపరితల వైశాల్యం = 2πrh
ఎత్తును రెట్టింపు, వ్యాసార్ధాన్ని 3 రెట్లు చేసిన స్థూపం ఉపరితల వైశాల్యం = 2π(3r)(2h)
= 12πrh = 6(2πrh)
కొత్త ఘనం ఉపరితల వైశాల్యం, మొదటి స్థూపం ఉపరితల వైశాల్యానికి 6 రెట్లు.

ప్రశ్న57.
x యూనిట్లు భుజంగా గల సమఘనంలో అంతర్లి ఖితమైన గోళం వ్యాసంను x లలో తెల్పండి.
జవాబు :
వ్యాసం d = x యూనిట్లు

ప్రశ్న58.
క్రింది వానిని జతపరచడంలో సరైన సమాధానాన్ని ఎన్నుకొనుము..

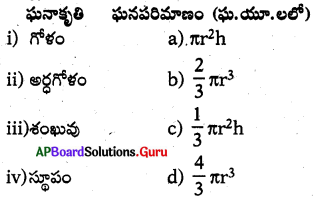
A) i-d, ii-b, iii-c, iv-a
B) i-a, ii-c, iii-b, iv-d
C) i-b, ii-a, iii-c, iv-d
D) i-d, ii-c, iii-b, iv-a
జవాబు :
A) i-d, ii-b, iii-c, iv-a

ప్రశ్న59.
అర్ధగోళం యొక్క సంపూర్ణతల వైశాల్యం కనుగొనుటకు సూత్రాన్ని రాయండి.
జవాబు :
అర్ధగోళ సంపూర్ణతల వైశాల్యం = 3πr²

ప్రశ్న60.
శంఖువు ఏటవాలు ఎత్తు l ను r, h లలో తెల్పండి.
జవాబు :
l = [latex]\sqrt{r^{2}+h^{2}}[/latex]

ప్రశ్న61.
ఒక సమఘనం యొక్క భుజాన్ని రెట్టింపు చేయగా, దాని ఘనపరిమాణం, మొదటి ఘనం ఘనపరిమాణానికి ఎన్ని రెట్లు ?
జవాబు :
ఘనం ఘనపరిమాణం = a³
a → 22 అయిన ఘనం ఘనపరిమాణం = (2a)³ = 8a³
కొత్త ఘనం ఘనపరిమాణం, మొదటి ఘనం ఘనపరిమాణంనకు 8 రెట్లు.

ప్రశ్న62.
ఒక లంబకోణ త్రిభుజాన్ని దాని కర్ణం పరంగా భ్రమణం చేస్తే అది ఏర్పరచు త్రిమితీయ ఆకారము ఏది ?
జవాబు :
శంఖువు

ప్రశ్న63.
గుల్ల అర్ధగోళాకార పాత్ర యొక్క లోపలి మరియు బయటి వ్యాసార్ధాలు వరుసగా r, R అయిన దాని సంపూర్ణతల . వైశాల్యం ………….
A) π(3R² + r²)
B) π(R² + r²)
C) π(R² + 3r²)
D) π(R² – r²)
జవాబు :
A) π(3R² + r²)

ప్రశ్న64.
10 సెం.మీ.లు వ్యాసార్థం గల ఒక గోళాన్ని 8 చిన్న సమాన గోళాలుగా మార్చగా చిన్న గోళాల యొక్క వ్యాసార్లమెంత ?
జవాబు :
చిన్న గోళ వ్యాసార్ధం r అనుకొనుము. 10 సెం.మీ. వ్యాసార్ధం గల గోళం ఘనపరిమాణం
= 8 చిన్న గోళాల మొత్తం ఘనపరిమాణం

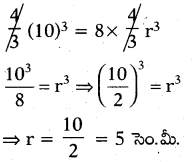
ప్రశ్న65.
శీర్షకోణం 60° గా గల శంఖువు యొక్క ఎత్తు, ఏటవాలు ఎత్తుల నిష్పత్తి ఎంత ?
జవాబు :

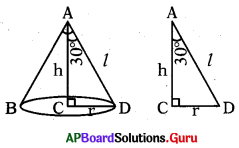
∠BAD = 60°; ∆ACDలో
cos 30° = [latex]\frac{\mathrm{AC}}{\mathrm{AD}} \Rightarrow \frac{\sqrt{3}}{2}=\frac{\mathrm{h}}{l}[/latex]
∴ h: 1 = √3 : 2,
(లేదా)
∆ACD లో కోణాలు 30°, 60, 90°.
భూజాల నిష్పత్తి r : h: 1 = 1 : √3 : 2
∴ h : 1 = √3 : 2

ప్రశ్న66.
శీర్షకోణం 60° గా గల శంఖువు భూవ్యాసార్ధ, ఎత్తుల నిష్పత్తి ఎంత ? (పై 65వ ప్రశ్న పటం చూడండి)
జవాబు :
tan 30° = [latex]\frac{\mathrm{r}}{\mathrm{h}} \Rightarrow \frac{1}{\sqrt{3}}=\frac{\mathrm{r}}{\mathrm{h}}[/latex]
∴ r : h = 1 : √3

ప్రశ్న67.
ఒక దీర్ఘఘనాకార ట్రక్కు నందు నింపగల – సంచుల సంఖ్యను లెక్కించడానికి క్రింది వానిలో దేనిని లెక్కించాలి ?
A) ప్రక్కతల వైశాల్యము
B) సంపూర్ణతల వైశాల్యము
C) ఘనపరిమాణము
D) భూతల వైశాల్యము
జవాబు :
C) ఘనపరిమాణము

ప్రశ్న68.
శంఖువు సంపూర్ణతల వైశాల్యంనకు సూత్రం తెల్పండి.
జవాబు :
శంఖువు సంపూర్ణతల వైశాల్యం = 4πr²

ప్రశ్న69.
స్థూపం సంపూర్ణతల వైశాల్యంను కనుగొనుటకు నీవు ఈ క్రింది వానిలో దేనిని ఎన్నుకుంటావు ?
A) 4πr²
B) 3πr²
C) 2πr (r + h)
D) πr (r +h)
జవాబు :
C) 2πr (r + h)

ప్రశ్న70.
అర్ధగోళం, సంపూర్ణతల వైశాల్యం, గోళం యొక్క సంపూర్ణతల వైశాల్యముల నిష్పత్తిని తెల్పండి.
జవాబు :
3πr² : 4πr² = 3 : 4

ప్రశ్న71.
సమాన వ్యాసార్ధాలు కలిగిన అర్ధగోళ సంపూర్ణతల వైశాల్యం, గోళ సంపూర్ణతల వైశాల్యములో ఎంత శాతము ఉంటుంది ?
జవాబు :
[latex]\frac{3 \pi r^{2}}{4 \pi r^{2}}[/latex] × 100 = 75%

ప్రశ్న72.
i) భూవ్యాసార్ధం 3 సెం.మీ., ఎత్తు 4 సెం.మీ.గా గల శంఖువు ఏటవాలు ఎత్తు 5 సెం.మీ.
ii) శంఖువు యొక్క భూవ్యాసార్ధం లో, ఎత్తు h గా గల శంఖువు ఏటవాలు ఎత్తు l = [latex]\sqrt{\mathbf{r}^{2}+\mathbf{h}^{2}}[/latex]
A) (i) సత్యం, (ii) సత్యం మరియు (i) కి (ii) సరైన వివరణ కాదు.
B) (i) సత్యం, (ii) సత్యం మరియు (i) & (ii) సరైన వివరణ.
C) (i) అసత్యం , (ii) సత్యం మరియు (i) కి (ii) . సరైన వివరణ.
D) (i) అసత్యం, (ii) అసత్యం మరియు (i) & (ii) సరైన వివరణ కాదు.
జవాబు :
B) (i) సత్యం, (ii) సత్యం మరియు (i) & (ii) సరైన వివరణ.

ప్రశ్న73.
ఒక వృత్తాకార స్థూపము యొక్క భూవ్యాసార్ధం 7 సెం.మీ. మరియు ఎత్తు 14 సెం.మీ. అయిన ఆ స్థూపం సంపూర్ణతల, వక్రతల వైశాల్యాల నిష్పత్తి ఎంత ?
జవాబు :
r = 7, h = 14 సంపూర్ణతల వైశాల్యం : వక్రతల వైశాల్యం

= r + h: h
= 7 + 14 : 14 = 21 : 14 = 3:2

ప్రశ్న74.
గోళం, స్థూపం, శంఖువు ఒకే వ్యాసార్ధాన్ని, ఎత్తును కలిగి ఉంటే వాటి యొక్క ఘనపరిమాణాల నిష్పత్తి ……
A) 1 : 2 : 3
B) 2 : 3 : 1
C) 3 : 2 : 1
D ) 3 : 1 : 2
జవాబు :
B) 2 : 3 : 1

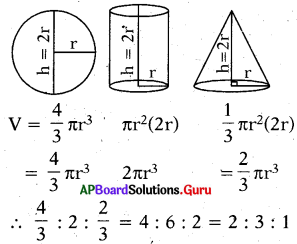
ప్రశ్న75.
ఒక వృత్తాకార స్థూపం వ్యాసార్ధం 6 సెం.మీ., ఎత్తు 7 సెం.మీ. అయిన దాని ఘనపరిమాణం ఎంత ?
జవాబు :
వృత్తాకార స్థూపం వ్యాసార్ధం r = 6, ఎత్తు h=7
ఘనపరిమాణం = πr²h = [latex]\frac{22}{7}[/latex] × (6)² × (7)
= 22 × 36
= 792 సెం.మీ.³

ప్రశ్న76.
పటంలోని A, B పాత్రలకు సంబంధించి క్రింది వానిలో ఏది సత్యము ?

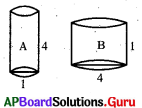
A) A పాత్ర యొక్క ఘనపరిమాణం B పాత్ర ఘనపరిమాణం కన్నా ఎక్కువ
B) A పాత్ర యొక్క ఘనపరిమాణం B పాత్ర ఘనపరిమాణం కన్నా తక్కువ
C) A, B పాత్రల యొక్క ఘనపరిమాణాలు సమానము
D) పైవి అన్నీ
జవాబు :
B) A పాత్ర యొక్క ఘనపరిమాణం B పాత్ర ఘనపరిమాణం కన్నా తక్కువ

ప్రశ్న77.
24 సెం.మీ. ఎత్తు, 6 సెం.మీ. భూవ్యాసార్ధము కలిగిన శంఖువు ఆకారంలోని మట్టిని, రిషి గోళముగా గల మట్టి ముద్దగా మార్చిన ఆ గోళం యొక్క వ్యాసార్ధము ఎంత ?
జవాబు :
శంఖువు ఎత్తు h = 24 సెం.మీ. ,
వ్యాసార్ధము r = 6 సెం.మీ., గోళం వ్యాసార్ధం r=?
గోళం ఘనపరిమాణం = శంఖువు ఘనపరిమాణం

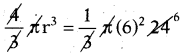
⇒ r³ = 6³
∴ r = 6 సెం.మీ.

ప్రశ్న78.
ఘనం ప్రక్కతల వైశాల్యం A = 4s², sను Aలలో తెల్పండి.
జవాబు :
4s² = A ⇒ s² = [latex]\frac{\mathrm{A}}{4}[/latex] ⇒ s = [latex]\sqrt{\frac{A}{4}}=\frac{\sqrt{A}}{2}[/latex]

ప్రశ్న79.
ఒక దీర్ఘ ఘనాకార బహుమతి పెట్టెను కప్పి ఉంచిన మెరుపు కాగిత వైశాల్యం కావలెనన్న దీర్ఘఘనం యొక్క క్రింది దేనిని లెక్కించాలి ?
A) ప్రక్కతల వైశాల్యము
B) సంపూర్ణతల వైశాల్యము
C) ఘనపరిమాణము
D) కర్ణము
జవాబు :
B) సంపూర్ణతల వైశాల్యము

ప్రశ్న80.
ఒక స్థూపము. మరియు శంఖువులు సమాన భూ వ్యాసార్ధములు మరియు ఎత్తులను కలిగి ఉంటే శంఖువు యొక్క ఘనపరిమాణం స్థూప ఘనపరిమాణంలో ఎంత శాతము ?
జవాబు :
స్థూపం, శంఖువుల ఘనపరిమాణముల నిష్పత్తి
= 3 : 1
∴ శంఖువు ఘనపరిమాణ శాతం = [latex]\frac{1}{3}[/latex] × 100
= 33[latex]\frac{1}{3}[/latex]%
∴ శంఖువు ఘనపరిమాణం, స్థూప ఘనపరిమాణంలో
33 % ఉంటుంది.

ప్రశ్న81.
గోళం సంపూర్ణతల వైశాల్యం A = 4πr² అయిన r విలువను Aలో రాయండి.
జవాబు :
4πr² = A ⇒ r² = [latex]\frac{\mathrm{A}}{4 \pi}[/latex]
⇒ r = [latex]\sqrt{\frac{\mathrm{A}}{4 \pi}}=\frac{1}{2} \sqrt{\frac{\mathrm{A}}{\pi}}[/latex]

ప్రశ్న82.
4 సెం.మీ. భుజంగా గల రెండు ఘనాలను ప్రక్కప్రక్కన కలుపబడిన క్రొత్తగా ఏర్పడిన దీర్ఘఘన సంపూర్ణతల వైశాల్యము ఎంత ?
జవాబు :
కొత్తగా ఏర్పడిన దీర్ఘఘన సంపూర్ణతల వైశాల్యం ,
= 10a² = 10(4)² = 160 చ.సెం.మీ.

ప్రశ్న83.
ఒక వృత్తాకార స్థూపం యొక్క ప్రక్కతల వైశాల్యం x ; భూ వైశాల్యము y; సంపూర్ణతల వైశాల్యం A అయిన A, x, y ల మధ్య సంబంధమును రాయండి.
జవాబు :
A = x + 2y

ప్రశ్న84.
ప్రవచనం-1 : స్థూపాకార పాత్రలో స్థూపాకార పాత్ర వ్యాసార్ధానికి సమాన వ్యాసార్ధం మరియు సమాన ఎత్తు కలిగిన గోళాన్ని అంతర్లీనపరిచిన గోళం యొక్క ఉపరితల వైశాల్యము, స్థూపం యొక్క వక్రతల వైశాల్యమునకు సమానము.
ప్రవచనం-II : పొడవు 1, వెడల్పు b, ఎత్తు h . యూనిట్లుగా గల దీర్ఘఘనం సంపూర్ణతల వైశాల్యం 2h(l + b) చ.యూనిట్లు.
A) I సత్యం, II అసత్యం
B) I అసత్యం, II సత్యం
C) I సత్యం మరియు II అసత్యం
D) I అసత్యం మరియు II అసత్యం
జవాబు :
C) I సత్యం మరియు II అసత్యం

ప్రశ్న85.
వాక్యం-a: ఘనాకార వస్తువుల సముదాయ ఉపరితల వైశాల్యము ఆ ఆకృతిలోని అన్ని ఘనాకార వస్తువుల ఉపరితల వైశాల్యముల మొత్తమునకు సమానము.
వాక్యం-b : ఘనాకార వస్తువు సముదాయ ఘన పరిమాణం, ఆ వస్తువులోని అన్ని ఘనాకార వస్తువుల ఘనపరిమాణముల మొత్తమునకు సమానము.
A) a – సత్యం, b – సత్యం
B) a – సత్యం, b – అసత్యం
C) a – అసత్యం మరియు b – సత్యం
D) a – అసత్యం మరియు b – అసత్యం
జవాబు :
C) a – అసత్యం మరియు b – సత్యం

ప్రశ్న86.
ఒక ఘనాకార వస్తువు అకృతిని, వేరొక ఘనాకార ఆకృతిగా మార్చిన వాని యొక్క క్రింది దేనిలో మార్పు ఉండదు ?
A) ఘనపరిమాణం
B) సంపూర్ణతల వైశాల్యము
C) ప్రక్కతల వక్రతల వైశాల్యం
D) భూవైశాల్యము
జవాబు :
A) ఘనపరిమాణం

ప్రశ్న87.
క్రింది పటంలో చూపిన స్థూపం మరియు శంఖువుల యొక్క వక్రతల వైశాల్యములు సమానం అయిన స్థూపం ఎత్తు l, శంఖువు ఏటవాలు ఎత్తు l ల నిష్పత్తి ఎంత ?

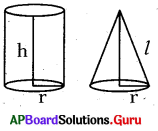
జవాబు :
స్థూపం వక్రతల వైశాల్యం = శంఖువు వక్రతల వైశాల్యం

⇒ [latex]\frac{\mathrm{h}}{l}=\frac{1}{2}[/latex] = h: 1 = 1 : 2

→ క్రింది ఆకృతుల చిత్తు పటాలు గీయండి (88-91)

ప్రశ్న88.
ఒక ఘనాకార వస్తువు ఒక చివర అర్ధగోళము, మరో చివర శంఖువు ఆకారము కలిగిన స్థూపము వలె ఉన్నది.
జవాబు :

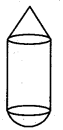
ప్రశ్న89.
ఒక నీటి ట్యాంకు రెండు చివరలా అర్ధగోళాకారము కలిగిన స్థూపాకారంలో కలదు.
జవాబు :

ప్రశ్న90.
ఒక ఆట వస్తువు అర్ధగోళం యొక్క సమతల ఉపరితలంపై క్రమ వృత్తాకార శంఖువు ఆకార భాగం యొక్క వృత్తాకార, భూభాగము కలుపబడి ఉన్నది.
జవాబు :

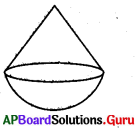
ప్రశ్న91.
శంఖువు ఆకార ఐస్ క్రీమ్ కోన్ ఐస్ క్రీం పైతలం అర్ధగోళాకారంలో ఉన్నట్లు. నింపబడినది.
జవాబు :

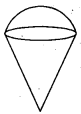
ప్రశ్న92.
10 లీటర్ల పరిమాణం కల్గిన నూనె డబ్బా యొక్క ఘనపరిమాణం (సెం.మీ.³) లో తెలపండి.
జవాబు :
10,000 సెం.మీ.³

ప్రశ్న93.
క్రింది ఇవ్వబడిన ప్రవచనాలలో సరైన జవాబును ఎన్నుకొనండి.
ప్రవచనం (A) : సమాన భూమి మరియు సమాన ఎత్తులు కల్గిన శంఖువు మరియు ‘స్థూపం ఘనపరిమాణాల నిష్పత్తి 3:1
ప్రవచనం (B) : సమాన భూమి మరియు సమాన ఎత్తులు కల్గిన గోళం మరియు శంఖువుల ఘనపరిమాణాల నిష్పత్తి 2 :1
i) A మరియు B లు రెండూ సత్యం
ii) A సత్యం , B అసత్యం
iii) A అసత్యం , B సత్యం
iv) A మరియు B లు రెండూ అసత్యాలే
జవాబు :
iv) A మరియు B లు రెండూ అసత్యాలే

ప్రశ్న94.
ఆహార ధాన్యాలను ఒకే భూమి పొడవు మరియు ఎత్తును కలిగిన కంటైనర్లలో నిల్వ చేయాలి. నిర్దిష్ట పరిమాణంలో ధాన్యాలను నిల్వ చేయడం కొరకు ఏ రకం కంటైనర్లు తక్కువ సంఖ్యలో అవసరం అవుతాయి ?
i) క్రమవృత్తాకార స్తూపం
ii) సమఘనం
iii) క్రమవృత్తాకార శంఖువు
జవాబు :
ii) సమఘనం

ప్రశ్న95.
ఒక దీర్ఘ ఘనాకార తెరచి ఉన్న వాటర్ ట్యాంకు బాహ్య కొలతలు పొడవు x యూనిట్లు, వెడల్పు y యూనిట్లు మరియు ఎత్తు 2 యూనిట్లు. గోడ యొక్క మందం ‘a’ యూనిట్లు అయితే, వాటర్ ట్యాంక్ లోపలి కొలతలు వ్యక్తీకరించండి.
జవాబు :
బాహ్య కొలతలు : పొడవు = x యూనిట్లు; వెడల్పు = y యూనిట్లు మరియు ఎత్తు = z యూనిట్లు. గోడ యొక్క మందం = a యూనిట్లు.
లోపలి కొలతలు :
పొడవు = x -a – a = x – 2a యూనిట్లు
(:: రెండు వైపుల గోడ మందము తీసివేయబడినది.)

వెడల్పు = y – a – a = y – 2a యూనిట్లు
(: రెండు వైపుల గోడ మందము తీసివేయబడినది.)

ఎత్తు = z – aయూనిట్లు (∵ పై భాగము తెరిచి యుండుట వలన క్రింది భాగము వెడల్పు మాత్రమే తీసివేయబడినది.)