SCERT AP 8th Class Maths Solutions Chapter 1 అకరణీయ సంఖ్యలు Ex 1.3 Textbook Exercise Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 1st Lesson అకరణీయ సంఖ్యలు Exercise 1.3
ప్రశ్న 1.
కింది వానిని [latex]\frac{p}{q}[/latex] రూపంలోకి వ్రాయండి.
(i) 0.57 (ii) 0.176 (iii) 1.00001 (iv) 25.125
సాధన.
(i) 0.57 = 0.57 లో దశాంశ స్థానంలో రెండంకెలు ఉన్నాయి. కావున దీనిని 100చే భాగించవలెను.
∴ 0.57 = [latex]\frac {57}{100}[/latex]
(Note : పాయింట్ తరువాత ఎన్ని అంకేలుంటే హారంలో అన్ని ‘సున్నా’లుండాలి.)
(ii) 0.176 = [latex]\frac {176}{1000}[/latex]
(iii) 1.00001 = [latex]\frac {100001}{100000}[/latex]
(iv) 25.125 = [latex]\frac {25125}{1000}[/latex]
ప్రశ్న 2.
ఈ కింది ఆవృత దశాంశాలను అకరణీయ సంఖ్యా రూపంలో వ్యక్తపరచండి. ([latex]\frac{p}{q}[/latex]).
(i) [latex]0 . \overline{9}[/latex] (ii) [latex]0 . \overline{57}[/latex] (iii) [latex]0.7 \overline{29}[/latex] (iv) [latex]12.2 \overline{8}[/latex]
సాధన.
(i) [latex]0 . \overline{9}[/latex]
x = 0.9 = 0.999 …….
⇒ x = 0.999 ……. ——- (1) లో 9 ఆవర్తితము.
దీని యొక్క అవధి 1.
∴ (1)వ సమీకరణాన్ని ఇరువైపులా 10చే గుణించగా
10 × x = 10 × 0.999 ……
10x = 9.999 …… —— (2)
x = [latex]\frac {9}{9}[/latex] = 1
∴ [latex]0 . \overline{9}[/latex] = 1
మరొక పద్ధతి :
[latex]0 . \overline{9}[/latex] = 0 + [latex]\overline{9}[/latex]
= 0 + [latex]\frac {9}{9}[/latex]
= 0 + 1 = 1
(ii) [latex]0 . \overline{57}[/latex]
x = [latex]0 . \overline{57}[/latex] = 0.5757 …….. —– (1)
ఇచ్చట అవధి 2 కావునా ఇరువైపులా ‘100’చే గుణించ వలెను.
⇒ 100 × x = 100 × 0.5757 …….
100x = 57.57 …… —– (2)
∴ x = [latex]\frac {57}{99}[/latex] లేదా x = [latex]\frac {19}{33}[/latex]
(iii) [latex]0.7 \overline{29}[/latex]
x = [latex]0.7 \overline{29}[/latex] = 0.72929 ….. —– (1)
ఇచ్చట అవధి 2 కావునా ఇరువైపులా (1)వ సమీకరణాన్ని 100చే గుణించగా
⇒ 100 × x = 100 × 0.72929 ……..
⇒ 100x = 72.9929 …… —– (2)
99x = 72.2
x = [latex]\frac {72.2}{99}[/latex] = [latex]\frac {722}{990}[/latex]
∴ x = [latex]\frac {361}{495}[/latex]
(iv) [latex]12.2 \overline{8}[/latex]
x = 12.288 …… …………..(1)
ఇచ్చట అవధి ‘1’ కావునా ఇరువైపులా ’10’చే గుణించగా
⇒ 10 × x = (12.288) × 10 ……
10x = 122.888 …… ……… (2)
3. కింద ఇచ్చిన విలువలకు (x + y) – (x – y) ను లెక్కించండి.
(i) x = [latex]\frac {5}{2}[/latex], y = -[latex]\frac {3}{4}[/latex]
(ii) x = [latex]\frac {1}{4}[/latex], y = [latex]\frac {3}{2}[/latex]
సాధన.
(i) x = [latex]\frac {5}{2}[/latex], y = -[latex]\frac {3}{4}[/latex] అయిన
(ii) x = [latex]\frac {1}{4}[/latex], y = [latex]\frac {3}{2}[/latex] అయిన
ప్రశ్న 4.
-[latex]\frac {13}{5}[/latex] మరియు [latex]\frac {12}{7}[/latex] ల మొత్తాన్ని -[latex]\frac {13}{7}[/latex] మరియు -[latex]\frac {1}{2}[/latex] ల లభించే భాగించండి.
సాధన.
-[latex]\frac {13}{5}[/latex] మరియు [latex]\frac {12}{7}[/latex] ల మొత్తం
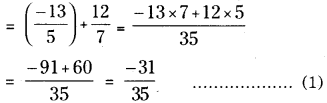
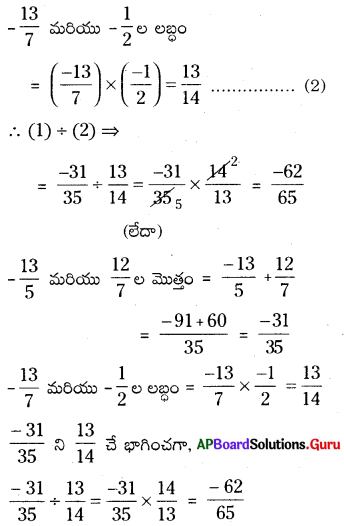
ప్రశ్న 5.
ఒక సంఖ్య యొక్క [latex]\frac {2}{5}[/latex] వ భాగం ఆ సంఖ్య యొక్క [latex]\frac {1}{7}[/latex] వ భాగం కంటే 36 ఎక్కువ అయిన ఆ సంఖ్యను కనుగొనుము.
సాధన.
ఒక సంఖ్య ‘x’ అనుకొనుము.
‘x’ యొక్క [latex]\frac {2}{5}[/latex] వ భాగం = [latex]\frac {2}{5}[/latex] × x = [latex]\frac{2 x}{5}[/latex]
x యొక్క [latex]\frac {1}{7}[/latex]వ భాగం = [latex]\frac {1}{7}[/latex] × x = [latex]\frac{x}{7}[/latex]
∴ లెక్క ప్రకారం
ప్రశ్న 6.
11 మీ. పొడవు గల తాడు నుండి 2[latex]\frac {3}{5}[/latex] మీ. మరియు 3[latex]\frac {3}{10}[/latex]మీ. పొడవులు గల రెండు ముక్కలు కత్తిరించగా మిగిలిన ముక్క పొడవు ఎంత ?
సాధన.
మిగిలిన తాడు ముక్క పొడవు
ప్రశ్న 7.
7[latex]\frac {2}{3}[/latex] మీటర్ల పొడవు గల ఒక గుడ్డ ఖరీదు ₹12[latex]\frac {3}{4}[/latex] అయిన ఒక మీటరు గుడ్డ ఖరీదు ఎంత ?
సాధన.
7[latex]\frac {2}{3}[/latex] మీ॥ల ([latex]\frac {23}{3}[/latex]మీ.) పొడవు గల గుడ్డ ఖరీదు
= ₹12[latex]\frac {3}{4}[/latex] = ₹[latex]\frac {51}{4}[/latex]
∴ 1 మీ. గుడ్డ ఖరీదు = [latex]\frac{51}{4} \div \frac{23}{3}[/latex]
= [latex]\frac {51}{4}[/latex] × [latex]\frac {3}{23}[/latex]
= [latex]\frac {153}{92}[/latex]
= ₹1.66
ప్రశ్న 8.
18[latex]\frac {3}{15}[/latex] మీ. పొడవు మరియు 8[latex]\frac {2}{3}[/latex]మీ. వెడల్పు గల ఒక దీర్ఘ చతురస్రాకార పార్క్ వైశాల్యం కనుగొనండి.
సాధన.
దీర్ఘచతురస్రాకార పార్క్
పొడవు = 18[latex]\frac {3}{15}[/latex] మీ. = [latex]\frac {93}{5}[/latex] మీ.
వెడల్పు = 8[latex]\frac {2}{3}[/latex] మీ. = [latex]\frac {26}{3}[/latex]మీ.
∴ దీర్ఘచతురస్రాకార పార్క్ వైశాల్యం (A) = l × b
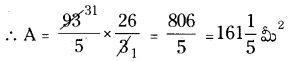
ప్రశ్న 9.
-[latex]\frac {33}{16}[/latex] ను ఏ సంఖ్యచే భాగించగా -[latex]\frac {11}{4}[/latex] వస్తుంది ?
సాధన.
భాగించవలసిన సంఖ్య ‘x’ అనుకొనుము.
ప్రశ్న 10.
64 మీటర్ల పొడవు గల ఒక బట్ట నుంచి సమాన పరిమాణం గల 36 ప్యాంటులు తయారుచేసిన ఒక్కొక్క , ప్యాంటు తయారుచేయుటకు ఎంత పొడవు గల బట్ట అవసరము ?
సాధన.
64 మీటర్ల పొడవు గల ఒక బట్ట నుంచి సమాన పరిమాణం గల 36 ప్యాంట్లు తయారుచేసిన ఒక్కొక్క ప్యాంటు తయారుచేయుటకు అవసరం అగు బట్ట పొడవు = 64 ÷ 36
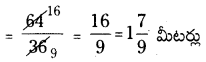
ప్రశ్న 11.
ఆవర్తిత దశాంశ సంఖ్య 10.363636… ను [latex]\frac{p}{q}[/latex] రూపంలో రాసిన p + q విలువ కనుగొనండి.
సాధన.
x = 10.363636 … ………………. (1)
ఇచ్చట అవధి 2.
(1)వ సమీకరణాన్ని ఇరువైపులా 100చే భాగించగా
⇒ 100 × x = 100 × 10.363636 …..
100x = 1036.36 … ……………… (2)
