AP State Syllabus AP Board 6th Class Maths Solutions Chapter 8 Basic Geometric Concepts Ex 8.3 Textbook Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 8th Lesson Basic Geometric Concepts Ex 8.3
Question 1.
Given ” [latex]\overline{\mathrm{AB}} / / \overline{\mathrm{CD}}[/latex], l ⊥ m”. Which are perpendicular? Which are parallel?
Solution:
are parallel lines (// is the symbol for parallel),
l, m are perpendicular lines (⊥ is the symbol for perpendicular).
Question 2.
Write the set of parallels and perpendiculars in the given by using symbols.
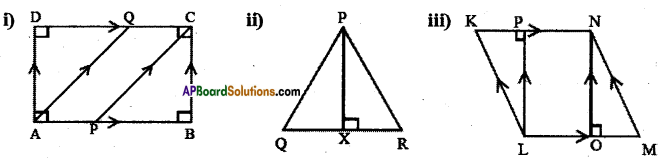
Solution:
a) [latex]\overline{\mathrm{AB}}, \overline{\mathrm{DC}}[/latex] are parallel lines, we denote this by writing [latex]\overline{\mathrm{AB}} / / \overline{\mathrm{DC}}[/latex] and can be read as [latex]\overline{\mathrm{AB}}[/latex] is parallel to [latex]\overline{\mathrm{DC}}[/latex]
b) [latex]\overline{\mathrm{AD}}, \overline{\mathrm{BC}}[/latex] are parallel lines. We denote this by writing [latex]\overline{\mathrm{AD}} / / \overline{\mathrm{BC}}[/latex] and can be read as [latex]\overline{\mathrm{AD}}[/latex] is parallel to [latex]\overline{\mathrm{BC}}[/latex]
c) [latex]\overline{\mathrm{AQ}}, \overline{\mathrm{PC}}[/latex] are parallel lines. We denote this by writing [latex]\overline{\mathrm{AQ}} / / \overline{\mathrm{PC}}[/latex] and can be read as [latex]\overline{\mathrm{AQ}}[/latex] is parallel to [latex]\overline{\mathrm{PC}}[/latex].
d) [latex]\overline{\mathrm{AB}}, \overline{\mathrm{AD}}[/latex] are perpendicular lines. We denote this by writing [latex]\overline{\mathrm{AB}} \perp \overline{\mathrm{AD}}[/latex] and can be read as [latex]\overline{\mathrm{AB}}[/latex] is perpendicular to [latex]\overline{\mathrm{AD}}[/latex].
e) [latex]\overline{\mathrm{AB}}, \overline{\mathrm{BC}}[/latex] are perpendicular lines. We denote this by writing [latex]\overline{\mathrm{AB}} \perp \overline{\mathrm{BC}}[/latex] and can be read as [latex]\overline{\mathrm{AB}}[latex] is perpendicular to [latex]\overline{\mathrm{BC}}[/latex] .
f) [latex]\overline{\mathrm{BC}}, \overline{\mathrm{CD}}[/latex] are perpendicular lines, we denote this by writing [latex]\overline{\mathrm{BC}} \perp \overline{\mathrm{CD}}[/latex] and can be read as [latex]\overline{\mathrm{BC}}[/latex] is perpendicular to [latex]\overline{\mathrm{CD}}[/latex].
g) [latex]\overline{\mathrm{CD}}, \overline{\mathrm{AD}}[/latex] are perpendicular lines, we denote this by writing [latex]\overline{\mathrm{CD}} \perp \overline{\mathrm{AD}}[/latex] and can be read as [latex]\overline{\mathrm{CD}}[/latex] is perpendicular to [latex]\overline{\mathrm{AD}}[/latex].
ii) [latex]\overline{\mathrm{PX}}, \overline{\mathrm{QR}}[/latex] are perpendicular lines, we denote this by writing [latex]\overline{\mathrm{PX}} \perp \overline{\mathrm{QR}}[/latex] and can be read as [latex]\overline{\mathrm{PX}}[/latex] is perpendicular to [latex]\overline{\mathrm{QR}}[/latex].
iii) a) [latex]\overline{\mathrm{LM}}, \overline{\mathrm{KN}}[/latex] are parallel lines. We denote this by writing [latex]\overline{\mathrm{LM}} / / \overline{\mathrm{KN}}[/latex] and can be read as [latex]\overline{\mathrm{LM}}[/latex] is parallel to [latex]\overline{\mathrm{KN}}[/latex].
b) [latex]\overline{\mathrm{MN}}, \overline{\mathrm{LK}}[/latex] are parallel lines. We denote this by writing [latex]\overline{\mathrm{MN}} / / \overline{\mathrm{LK}}[/latex] and can be read as [latex]\overline{\mathrm{MN}}[/latex] is parallel to [latex]\overline{\mathrm{LK}}[/latex].
c) [latex]\overline{\mathrm{ON}}, \overline{\mathrm{LP}}[/latex] are parallel lines. We denote this by writing [latex]\overline{\mathrm{ON}} / / \overline{\mathrm{LP}}[/latex] and can be read
as [latex]\overline{\mathrm{ON}}[/latex] is parallel to [latex]\overline{\mathrm{LP}}[/latex]
d) [latex]\overline{\mathrm{LM}}, \overline{\mathrm{ON}}[/latex] are perpendicular lines, we denote this by writing [latex]\overline{\mathrm{ON}} \perp \overline{\mathrm{LM}}[/latex] and can be read as [latex]\overline{\mathrm{ON}}[/latex] is perpendicular to [latex]\overline{\mathrm{LM}}[/latex].
e) [latex]\overline{\mathrm{LP}}, \overline{\mathrm{KN}}[/latex] are perpendicular lines, we denote this by writing [latex]\overline{\mathrm{LP}} \perp \overline{\mathrm{KN}}[/latex] and can be read as [latex]\overline{\mathrm{LP}}[/latex] is perpendicular to [latex]\overline{\mathrm{KN}}[/latex].
Question 3.
From the given figure find out the Intersecting lines and concurrent lines.
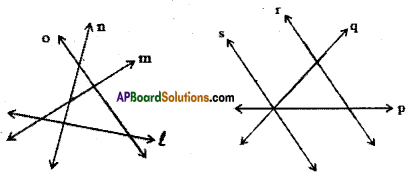
Solution:
i) Intersecting lines : (l, m); (l, n); (n, o); (m, o); (l, o); (m, n)
ii) Intersecting lines: (p, q); (p, r); (p, s); (q, r); (q, s)
Concurrent lines : (p, q, s)