Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Matrices Solutions Exercise 3(d) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1A Matrices Solutions Exercise 3(d)
I.
Question 1.
Find the determinants of the following matrices.
(i) [latex]\left[\begin{array}{cc}
2 & 1 \\
1 & -5
\end{array}\right][/latex]
Solution:
det A = ad – bc
= 2(-5) – 1(1)
= -10 – 1
= -11
(ii) [latex]\left[\begin{array}{cc}
4 & 5 \\
-6 & 2
\end{array}\right][/latex]
Solution:
det A = 4(2) – (-6)(5)
= 8 + 30
= 38
(iii) [latex]\left[\begin{array}{cc}
\mathbf{i} & 0 \\
0 & -\mathbf{i}
\end{array}\right][/latex]
Solution:
det A = -i2 – 0
= 1 – 0
= 1
![]()
(iv) [latex]\left[\begin{array}{lll}
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0
\end{array}\right][/latex]
Solution:
det A = 0(0 – 1) – 1(0 – 1) + 1(1 – 0)
= 1 + 1
= 2
(v) [latex]\left[\begin{array}{ccc}
1 & 4 & 2 \\
2 & -1 & 4 \\
-3 & 7 & 6
\end{array}\right][/latex]
Solution:
det A = 1(-6 – 28) – 4(12 + 12) + 2(14 – 3)
= -34 – 96 + 22
= -108
(vi) [latex]\left[\begin{array}{ccc}
2 & -1 & 4 \\
4 & -3 & 1 \\
1 & 2 & 1
\end{array}\right][/latex]
Solution:
det A = 2(-3 – 2) + 1(4 – 1) + 4(8 + 3)
= -10 + 3 + 44
= 37
(vii) [latex]\left[\begin{array}{ccc}
1 & 2 & -3 \\
4 & -1 & 7 \\
2 & 4 & -6
\end{array}\right][/latex]
Solution:
det A = 0 since R1 and R3 are proportional.
![]()
(viii) [latex]\left[\begin{array}{lll}
a & h & g \\
\text { h } & b & f \\
g & f & c
\end{array}\right][/latex]
Solution:
det A = a(bc – f2) – h(ch – fg) + g(hf – bg)
= abc – af2 – ch2 + fgh + fgh – bg2
= abc + 2fgh – af2 – bg2 – ch2
(ix) [latex]\left[\begin{array}{lll}
\mathbf{a} & \mathbf{b} & \mathbf{c} \\
\mathbf{b} & \mathbf{c} & \mathbf{a} \\
\mathbf{c} & \mathbf{a} & \mathbf{b}
\end{array}\right][/latex]
Solution:
det A = a(bc – a2) – b(b2 – ac) + c(ab – c2)
= abc – a3 – b3 + abc + abc – c3
= 3abc – a3 – b3 – c3
(x) [latex]\left[\begin{array}{ccc}
1^{2} & 2^{2} & 3^{2} \\
2^{2} & 3^{2} & 4^{2} \\
3^{2} & 4^{2} & 5^{2}
\end{array}\right][/latex]
Solution:
det A = [latex]\left|\begin{array}{ccc}
1 & 4 & 9 \\
4 & 9 & 16 \\
9 & 16 & 25
\end{array}\right|[/latex]
= 1(225 – 256) – 4(100 – 144) – 9(64 – 81)
= -31 + 176 – 153
= -184 + 176
= -8
Question 2.
If A = [latex]\left[\begin{array}{ccc}
1 & 0 & 0 \\
2 & 3 & 4 \\
5 & -6 & x
\end{array}\right][/latex] and det A = 45 then find x.
Solution:
det A = 45
[latex]\left|\begin{array}{ccc}
1 & 0 & 0 \\
2 & 3 & 4 \\
5 & -6 & x
\end{array}\right|[/latex] = 45
⇒ 3x + 24 = 45
⇒ 3x – 45 + 24 = 0
⇒ 3x – 21 = 0
⇒ x = 7
![]()
II.
Question 1.
Show that [latex]\left|\begin{array}{lll}
b c & b+c & 1 \\
c a & c+a & 1 \\
a b & a+b & 1
\end{array}\right|[/latex] = (a – b)(b – c)(c – a)
Solution:

Question 2.
Show that [latex]\left|\begin{array}{ccc}
\mathbf{b}+\mathbf{c} & \mathbf{c}+\mathbf{a} & \mathbf{a}+\mathbf{b} \\
\mathbf{a}+\mathbf{b} & \mathbf{b}+\mathbf{c} & \mathbf{c}+\mathbf{a} \\
\mathbf{a} & \mathbf{b} & \mathbf{c}
\end{array}\right|[/latex] = a3 + b3 + c3 – 3abc
Solution:
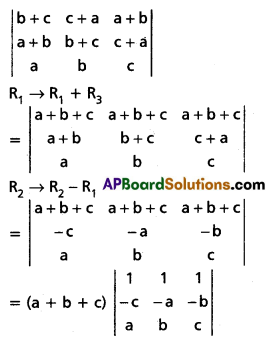
= (a + b + c) [(-ac + b2) – (-c2 + ab) + (-bc + a2)]
= (a + b + c) (-ac + b2 + c2 – ab – bc + a2)
= (a + b + c) (a2 + b2 + c2 – ab – bc – ca)
= a3 + b3 + c3 – 3abc
Question 3.
Show that [latex]\left|\begin{array}{ccc}
\mathbf{y}+\mathbf{z} & \mathbf{x} & \mathbf{x} \\
\mathbf{y} & \mathbf{z}+\mathbf{x} & \mathbf{y} \\
\mathbf{z} & \mathbf{z} & \mathbf{x}+\mathbf{y}
\end{array}\right|[/latex] = 4xyz
Solution:
L.H.S = [latex]\left|\begin{array}{ccc}
\mathbf{y}+\mathbf{z} & \mathbf{x} & \mathbf{x} \\
\mathbf{y} & \mathbf{z}+\mathbf{x} & \mathbf{y} \\
\mathbf{z} & \mathbf{z} & \mathbf{x}+\mathbf{y}
\end{array}\right|[/latex]
= (y + z) [(z + x) (x + y) – yz] – x[y(x + y) – yz] + x[yz – z(z + x)]
= (y + z) (zx + yz + x2 + xy – yz) – x(xy + y2 – yz) + x(yz – z2 – zx)
= (y + z) (zx + x2 + xy) – x(xy + y2 – yz) + x(yz – z2 – zx)
= xyz + x2y + xy2 + xz2 + x2z + xyz – x2y – xy2 + xyz + xyz – xz2 – x2z
= 4xyz
= R.H.S
Question 4.
If [latex]\left|\begin{array}{ccc}
a & a^{2} & 1+a^{3} \\
b & b^{2} & 1+b^{3} \\
c & c^{2} & 1+c^{3}
\end{array}\right|[/latex] = 0 and [latex]\left|\begin{array}{ccc}
a & a^{2} & 1 \\
b & b^{2} & 1 \\
c & c^{2} & 1
\end{array}\right|[/latex] ≠ 0 then show that abc = -1
Hint: If each element in a row (column) of a square matrix is the sum of two numbers, then its discriminant can be expressed as the sum of discriminants of two square matrices.
Solution:
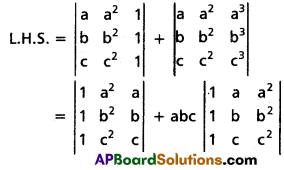
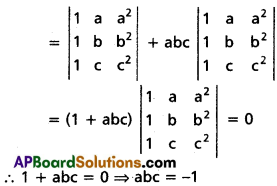
Question 5.
Without expanding the determinant, prove that
(i) [latex]\left|\begin{array}{ccc}
a & a^{2} & b c \\
b & b^{2} & c a \\
c & c^{2} & a b
\end{array}\right|=\left|\begin{array}{ccc}
1 & a^{2} & a^{3} \\
1 & b^{2} & b^{3} \\
1 & c^{2} & c^{3}
\end{array}\right|[/latex]
Solution:

(ii) [latex]\left|\begin{array}{ccc}
a x & b y & c z \\
x^{2} & y^{2} & z^{2} \\
1 & 1 & 1
\end{array}\right|=\left|\begin{array}{ccc}
a & b & c \\
x & y & z \\
y z & z x & x y
\end{array}\right|[/latex]
Solution:
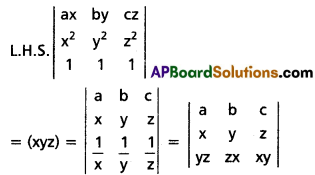
(iii) [latex]\left|\begin{array}{lll}
1 & b c & b+c \\
1 & c a & c+a \\
1 & a b & a+b
\end{array}\right|=\left|\begin{array}{ccc}
1 & a & a^{2} \\
1 & b & b^{2} \\
1 & c & c^{2}
\end{array}\right|[/latex]
Solution:
L.H.S = [latex]\left|\begin{array}{ccc}
1 & b c & b+c \\
1 & c a & c+a \\
1 & a b & a+b
\end{array}\right|[/latex]

= (b – a) (c – a) (c + a – b – a)
= (a – b) (b – c) (c – a)
∴ LHS = RHS
![]()
Question 6.
If ∆1 = [latex]\left|\begin{array}{ccc}
a_{1}^{2}+b_{1}+c_{1} & a_{1} a_{2}+b_{2}+c_{2} & a_{1} a_{3}+b_{3}+c_{3} \\
b_{1} b_{2}+c_{1} & b_{2}^{2}+c_{2} & b_{2} b_{3}+c_{3} \\
c_{3} c_{1} & c_{3} c_{2} & c_{3}^{2}
\end{array}\right|[/latex] and ∆2 = [latex]\left|\begin{array}{lll}
a_{1} & b_{2} & c_{2} \\
a_{2} & b_{2} & c_{2} \\
a_{3} & b_{3} & c_{3}
\end{array}\right|[/latex], then find the value of [latex]\frac{\Delta_{1}}{\Delta_{2}}[/latex]
Solution:


Question 7.
If ∆1 = [latex]\left|\begin{array}{ccc}
1 & \cos \alpha & \cos \beta \\
\cos \alpha & 1 & \cos \gamma \\
\cos \beta & \cos \alpha & 1
\end{array}\right|[/latex], ∆2 = [latex]\left|\begin{array}{ccc}
0 & \cos \alpha & \cos \beta \\
\cos \alpha & 0 & \cos \gamma \\
\cos \beta & \cos \gamma & 0
\end{array}\right|[/latex] and ∆1 = ∆2, then show that cos2α + cos2β + cos2γ = 1
Solution:
∆1 = [latex]\left|\begin{array}{ccc}
1 & \cos \alpha & \cos \beta \\
\cos \alpha & 1 & \cos \gamma \\
\cos \beta & \cos \alpha & 1
\end{array}\right|[/latex]
= 1(1 – cos2γ) – cos α (cos α – cos β cos γ) + cos β (cos α cos γ – cos β)
= 1 – cos2γ – cos2α + cos α cos β cos γ + cos α cos β cos γ – cos2β
= 1 – cos2γ – cos2α – cos2β + 2 cos α cos β cos γ
∆2 = [latex]\left|\begin{array}{ccc}
0 & \cos \alpha & \cos \beta \\
\cos \alpha & 0 & \cos \gamma \\
\cos \beta & \cos \gamma & 0
\end{array}\right|[/latex]
= 0(0 – cos2γ) – cos α (0 – cos γ cos β) + cos β (cos α cos γ – 0)
= cos α cos β cos γ + cos α cos β cos γ
= 2 cos α cos β cos γ
Given ∆1 = ∆2
1 – cos2α – cos2β – cos2γ + 2 cos α cos β cos γ = 2 cos α cos β cos γ
1 – cos2α – cos2β – cos2γ = 0
1 = cos2α + cos2β + cos2γ
![]()
III.
Question 1.
Show that [latex]\left|\begin{array}{ccc}
\mathbf{a}+\mathbf{b}+2 \mathbf{c} & \mathbf{a} & \mathbf{b} \\
\mathbf{c} & \mathbf{b}+\mathbf{c}+\mathbf{2} \mathbf{a} & \mathbf{b} \\
\mathbf{c} & \mathbf{a} & \mathbf{c}+\mathbf{a}+\mathbf{2} \mathbf{b}
\end{array}\right|[/latex] = 2(a + b + c)3
Solution:

Question 2.
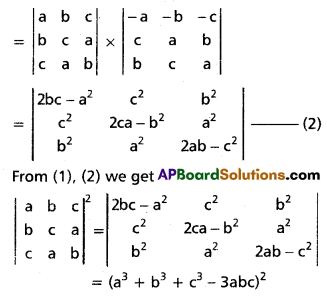
Show that [latex]\left|\begin{array}{lll}
a & b & c \\
b & c & a \\
c & a & b
\end{array}\right|^{2}[/latex] = [latex]\left|\begin{array}{ccc}
2 b c-a^{2} & c^{2} & b^{2} \\
c^{2} & 2 a c-b^{2} & a^{2} \\
b^{2} & a^{2} & 2 a b-c^{2}
\end{array}\right|[/latex] = (a3 + b3 + c3 – 3abc)2
Solution:

Question 3.
Show that [latex]\left|\begin{array}{ccc}
a^{2}+2 a & 2 a+1 & 1 \\
2 a+1 & a+2 & 1 \\
3 & 3 & 1
\end{array}\right|[/latex] = (a – 1)3
Solution:

![]()
Question 4.
Show that [latex]\left|\begin{array}{ccc}
a & b & c \\
a^{2} & b^{2} & c^{2} \\
a^{3} & b^{3} & c^{3}
\end{array}\right|[/latex] = abc(a – b)(b – c)(c – a)
Solution:

Question 5.
Show that [latex]\left|\begin{array}{ccc}
-2 \mathbf{a} & \mathbf{a}+\mathbf{b} & \mathbf{c}+\mathbf{a} \\
\mathbf{a}+\mathbf{b} & -\mathbf{2} \mathbf{b} & \mathbf{b}+\mathbf{c} \\
\mathbf{c}+\mathbf{a} & \mathbf{c}+\mathbf{b} & -2 \mathbf{c}
\end{array}\right|[/latex] = 4(a + b) (b + c) (c + a)
Solution:

∴ (c + a) is a factor for ∆
Similarly a + b, b + c are also factors ∆.
∵ ∆ is a third-degree expression in a, b, c.
∆ = k(a + b) (b + c) (c + a),
where k is a non-zero scalar.
Put a = 1, b = 1, c = 1, then
[latex]\left|\begin{array}{ccc}
-2 & 2 & 2 \\
2 & -2 & 2 \\
2 & 2 & -2
\end{array}\right|[/latex] = k(1 + 1) (1 + 1) (1 + 1)
⇒ -2(4 – 4) – 2(-4 – 4) + 2(4 + 4) = 8k
⇒ 16 + 16 = 8k
⇒ k = 4
∴ ∆ = 4(a + b) (b + c) (c + a)
Hence [latex]\left|\begin{array}{ccc}
-2 \mathbf{a} & \mathbf{a}+\mathbf{b} & \mathbf{c}+\mathbf{a} \\
\mathbf{a}+\mathbf{b} & -\mathbf{2} \mathbf{b} & \mathbf{b}+\mathbf{c} \\
\mathbf{c}+\mathbf{a} & \mathbf{c}+\mathbf{b} & -2 \mathbf{c}
\end{array}\right|[/latex] = 4(a + b) (b + c) (c + a)
![]()
Question 6.
Show that [latex]\left|\begin{array}{lll}
\mathbf{a}-\mathbf{b} & \mathbf{b}-\mathbf{c} & \mathbf{c}-\mathbf{a} \\
\mathbf{b}-\mathbf{c} & \mathbf{c}-\mathbf{a} & \mathbf{a}-\mathbf{b} \\
\mathbf{c}-\mathbf{a} & \mathbf{a}-\mathbf{b} & \mathbf{b}-\mathbf{c}
\end{array}\right|[/latex]
Solution:
L.H.S = [latex]\left|\begin{array}{ccc}
0 & 0 & 0 \\
b-c & c-a & a-b \\
c-a & a-b & b-c
\end{array}\right|[/latex] = 0
By R1 → R1 + (R2 + R3)
Question 7.
Show that [latex]\left|\begin{array}{ccc}
1 & a & a^{2}-b c \\
1 & b & b^{2}-c a \\
1 & c & c^{2}-a b
\end{array}\right|[/latex] = 0
Solution:

Question 8.
Show that [latex]\left|\begin{array}{lll}
\mathbf{x} & \mathbf{a} & \mathbf{a} \\
\mathbf{a} & \mathbf{x} & \mathbf{a} \\
\mathbf{a} & \mathbf{a} & \mathbf{x}
\end{array}\right|[/latex] = (x + 2a) (x – a)2
Solution:
