AP Board 9th Class Maths Solutions Chapter 11 Areas Ex 11.1

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 11 Areas Ex 11.1 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 11th Lesson Areas Exercise 11.1

Question 1.
In ΔABC, ∠ABC = 90°; AD = DC; AB =12 cm, BC = 6.5 cm. Find the area of ΔADB

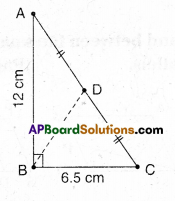
Solution:
ΔADB = [latex]\frac { 1 }{ 2 }[/latex] ΔABC [ ∵ AD is a median of ΔABC]
[latex]\frac { 1 }{ 2 }[/latex] = [ [latex]\frac { 1 }{ 2 }[/latex] AB x BC]
= [latex]\frac { 1 }{ 4 }[/latex] x 12 x 6.5
= 19.5 cm²

Question 2.
Find the area of a quadrilateral PQRS in which ∠QPS = ∠SQR = 90°, PQ = 12 cm, PS = 9 cm, QR = 8 cm and SR =17 cm.
[Hint: PQRS has two parts]

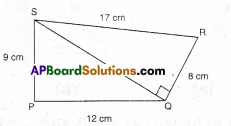
Solution:
Area of ΔQPS = [latex]\frac { 1 }{ 2 }[/latex] x base x height
= [latex]\frac { 1 }{ 2 }[/latex] x 9 x 12
= 54cm²
In ΔQPS
QS² = PQ² + PS²
QS = [latex]\begin{aligned}
\sqrt{12^{2}+9^{2}} &=\sqrt{144+81} \\
&=\sqrt{225}=15
\end{aligned}[/latex]
Area of ΔQSR =[latex]\frac { 1 }{ 2 }[/latex] x base x height
= [latex]\frac { 1 }{ 2 }[/latex] x 15 x 8 = 60 cm²
∴ □PQRS = ΔQPS + ΔQSR
= 54 + 60= 114 cm²

Question 3.
Find the area of trapezium ABCD as given in the figure in which ADCE is a rectangle.
[Hint: ABCD has two parts]

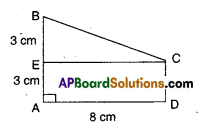
Solution:
Area of trapezium 1
= [latex]\frac { 1 }{ 2 }[/latex] (sum of parallel sides) x (distance between the parallel sides)
= [latex]\frac { 1 }{ 2 }[/latex] (a + b) h
From the figure, a = 3 + 3 = 6 cm
b = 3 cm
(∵ Opp. sides of rectangle)
h = 8 cm
∴ A = [latex]\frac { 1 }{ 2 }[/latex](6 + 3)x8 = 36cm²

Question 4.
ABCD is a parallelogram. The diago-nals AC and BD intersect each other at O. Prove that ar (ΔAOD) = ar (ΔBOQ. [Hint: Congruent figures have equal area]

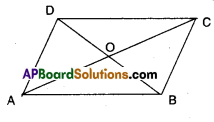
Solution:
Given that □ABCD is a parallelogram.
Diagonals AC and BD meet at ‘O’.
In ΔAOD and ΔBOC
AD = BC [ ∵ Opp. sides of a ||gm]
AO = OC [ ∵ diagonals bisect each
OD = OB other]
ΔAOD = ΔBOC [S.S.S. congruence]
∴ ΔAOD = ΔBOC (i.e., have equal area)