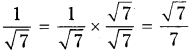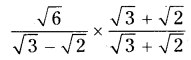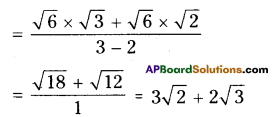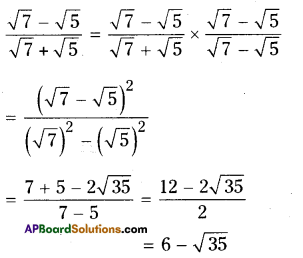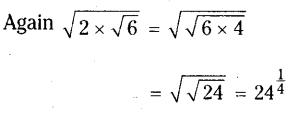Srinivas

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 2 Polynomials and Factorisation Ex 2.5 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 2nd Lesson Polynomials and Factorisation Exercise 2.5

Question 1.
Use suitable identities to find the following products.
i) (x + 5) (x + 2)
Solution:
(x + 5) (x + 2)
= x² + (5 + 2)x + 5 x 2
[ ∵ (x + a) (x + b) = x² + (a + b) x + ab]
= x² + 7x + 10

ii) (x – 5) (x – 5)
Solution:
(x – 5) (x – 5)
= (x – 5)² = x² – 2(x) (5) + 5²
[ ∵(x – y)² = x² – 2xy + y²]
= x² – 10x + 25

iii) (3x + 2) (3x – 2)
Solution:
(3x + 2) (3x – 2) = (3x)² – (2)²
[∵ (x + y) (x – y) =x² – y²]
= 9x² – 4

iv) \(\left(x^{2}+\frac{1}{x^{2}}\right)\left(x^{2}-\frac{1}{x^{2}}\right)\)
Solution:

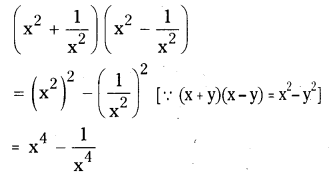
v) (1 + x) (1 + x)
Solution:
(1 + x) (1 + x)
= (1 + x)² = 1² + 2 (1) (x) + x²
[∵(x + y)² = x² + 2xy + y²]
= 1 + 2x + x²

Question 2.
Evaluate the following products with¬out actual multiplication.
i) 101 x 99
Solution:
101 x 99
= (100 + 1) (100 – 1)
= 100² – 1²
= 10000 – 1
= 9999

ii) 999 x 999
Solution:
999 x 999
= 999²
= (1000 – 1)²
= 1000² – 2 x (1000) x 1 + 1²
= 1000000-2000 + 1
= 998001

iii) \(50 \frac{1}{2} \times 49 \frac{1}{2}\)
Solution:

iv) 501 x 501
Solution:
501 x 501
= (500 + 1) (500 + 1)
= (500 + 1)²
= 500² + 2 x (500) x 1 + 1²
= 250000 + 1000 + 1 = 251001

v) 30.5 x 29.5 = (30 + 0.5) (30 – 0.5)
= 30² – (0.5)²
= 900 – 0.25
= 899.75

Question 3.
Factorise the following using appro-priate identities.
i) 16x² + 24xy + 9y²
Solution:
16x² + 24xy + 9y2
= (4x)² + 2 (4x) (3y) + (3y)²
= (4x + 3y)² = (4x + 3y) (4x + 3y)
[ ∵ (x + y)² = x² + 2xy + y²]

ii) 4y² – 4y + 1
Solution:
4y² – 4y + 1
= (2y)² – 2 (2y) (1) + (1)²
[ ∵ (x -y)² = x² – 2xy + y²]
= (2y -1)² = (2y – 1) (2y-1)

iii) \(4 x^{2}-\frac{y^{2}}{25}\)
Solution:

iv) 18a² – 50
Solution:
18a² – 50 = 2 (9a² – 25)
= 2[(3a)² – (5)²]
[ ∵ x² – y² = (x + y) (x – y)]
= 2 (3a + 5) (3a – 5)

v) x² + 5x + 6
Solution:
x² + 5x + 6 = x² + (3 + 2) x + 3 x 2
[ ∵ (x + a) (x + b) = x² + (a + b) x + a . b]
= (x + 3) (x + 2)

vi) 3p² – 24p + 36
Solution:
3p² – 24p + 36
= 3[p² – 8p + 12]
= 3[p² + (- 6 – 2)p + (- 6) (- 2)]
[ ∵ (x + a) (x + b) = x² + (a + b) x + ab]
= 3 (p – 6) (p – 2)

Question 4.
Expand each of the following, using suitable identities.
i) (x + 2y + 4z)2
(x + 2y + 4z)² = (x)² + (2y)² + (4z)² + 2(x) (2y) + 2 (2y) (4z) + 2 (4z) (x)
[ ∵ (x + y + z)² = x² + y² + z² + 2xy + 2yz + 2zx]
= x² + 4y² + 16z² + 4xy + 16yz + 8zx

ii) (2a – 3b)³
Solution:
(2a – 3b)³ = (2a)³ – 3 (2a)² (3b) + 3 (2a) (3b)² – (3b)³
[ ∵ (a – b)³ = a³ – 3a²b + 3ab² – b³]
= 8a³ – 3(4a²) (3b) + 3 (2a) (9b²) – 27b³
= 8a³ – 36a²b + 54ab²-27b³
(or)
∵ (a – b)³ = a³ – b³– 3ab (a – b)]
= (2a)³ – (3b)³ – 3(2a) (3b) (2a – 3b)
= 8a³ – 27b³ – 18ab (2a – 3b)

iii) (- 2a + 5b – 3c)²
Solution:
(- 2a + 5b – 3c)²
= (- 2a)² + (5b)² + (- 3c)² + 2 (- 2a) (5b) + 2 (5b) (- 3c) + 2 (- 3c) (- 2a)
= 4a² + 25b² + 9c² – 20ab – 30bc + 12ca
[ ∵ (x + y + z)² = x² + y² + z² + 2xy +2yz +2za]

iv) \(\left[\frac{a}{4}-\frac{b}{2}+1\right]^{2}\)
Solution:

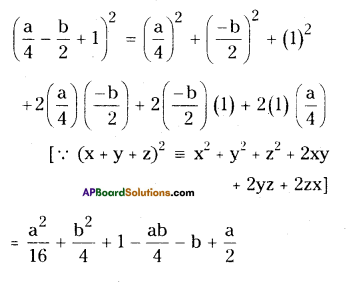
v) (p + 1)³
Solution:
(p + 1)³
= (P)³ + 3 (p)² (1) + 3 (p) (1)² + (1)³
[ ∵ (x + y)³ = x³ + 3x²y + 3xy² + y³]
= p³ + 3p² + 3p + 1

vi) \(\left(x-\frac{2}{3} y\right)^{3}\)
Solution:

Question 5.
Factorise
i) 25x² + 16y² + 4z² – 40xy + 16yz – 20xz
Solution:
25x² + 16y² + 4z² – 40xy + 16yz – 20xz
= (5x)² + (- 4y)² + (- 2z)² + 2(5x) (- 4y) + 2 (- 4y) (- 2z) + 2 (- 2z) (5x)
= (5x – 4y – 2z)² = (- 5x + 4y +, 2z)²

ii) 9a² + 4b² + 16c² + 12ab – 16bc – 24ca
Solution:
9a² + 4b² + 16c² + 12ab – 16bc -24ca
= (3a)² + (2b)² + (- 4c)²+ 2 (3a) (2b) + 2 (2b) (- 4c) + 2(- 4c) (3a)
= (3a + 2b – 4c)²

Question 6.
If a + b + c = 9 and ab + be + ca = 26, find a² + b² + c².
Solution:
Given that a + b + c = 9
Squaring on both sides,
(a + b + c)² = 9²
⇒ a²+ b² + c²+ 2 (ab + be + ca) = 81 ⇒ a² + b² + c² = 81 – 2 (ab + be + ca)
(by problem)
= 81 – 2 x 26
= 81 – 52 = 29

Question 7.
Evaluate the following by using suit¬able identities. m EachgM)
i) (99)³
Solution:
(99)² = (100 – 1)³
= 100³ – 3 (100)² (1) + 3 (100) (1)² – 1³
[ ∵ (x – y)³ = x³ – 3x²y + 3xy² + y³]
= 1000000 – 30000 + 300 – 1
= 970299

ii) (102)³
Solution:
(102)³ = (100 + 2)³
= 100³ + 3 (100)² (2) + 3 (100) (2)² + 2³
[ ∵ (x + y)³ = x³ + 3x²y + 3xy² + y³]
= 1000000 + 60000 + 1200 + 8
= 1061208

iii) (998)³
Solution:
(998)³ =(1000 – 2)³
[ ∵ (x – y)³ = x³ – 3x²y + 3xy² – y³] = 1000³– 3(1000)²(2) + 3(1000)(2)²– 2³
= 1000000000 – 6000000 + 12000 – 8
= 994011992

iv) (1001)³
Solution:
(1001)³ = (1000 + 1)³ .
[ ∵ (x + y)³ = x³ + 3x²y + 3xy² + y³] = 1000³ + 3(1000)²(1) + 3(1000) (1)² + 1³
= 1000000000 + 3000000 + 3000 + 1
= 1003003001

Question 8.
Factorise each of the following.
i) 8a³ + b³ + 12a² b + 6ab²
Solution:
8a³ + b³ + 12a² b + 6ab²
= (2a)³ + (b)³ + 3 (2a)² (b) + 3 (2a) (b)²
= (2a + b)³

ii) 8a³ – b³ – 12a² b + 6ab²
Solution:
8a³ – b³ – 12a² b + 6ab²
= (2a)³ – (b)³ – 3 (2a)² (b) + 3 (2a) (b)²
= (2a – b)³

iii) 1 – 64a³ -12a + 48a²
Solution:
1 – 64a³ – 12a + 48a²
= (1)³ – (4a)³ – 3(1)² (4a) + 3(1) (4a)²
= (1 – 4a)³

iv) \(8 p^{3}-\frac{12}{5} p^{2}+\frac{6}{25} p-\frac{1}{125}\)
Solution:

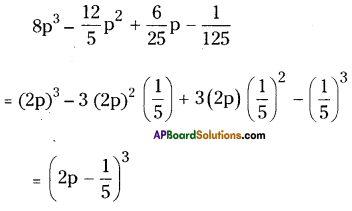
Question 9.
Verify i) x³ + y³ = (x + y) (x² – xy + y²);
ii) x³ – y³ = (x – y) (x² + xy + y²)
Using some non-zero positive integers and check by actual multiplication. Can you
call these as identities ?
i) x³ + y³ = (x + y) (x² – xy + y²)
Solution:
Given x³ + y³ = (x + y) (x² – xy + y²)
L.H.S = x³ + y³
R.H.S = (x + y) (x² – xy + y²)
= x (x² – xy + y²) + y (x² – xy + y²)
= x³ -x²y + xy² + x²y – xy² + y³
= x³ + y³
= L.H.S
∴ L.H.S = R.H.S

Take x = 3, y = 2
L.H.S = 3³ + 2³ = 27 + 8 = 35
R.H.S = (3 + 2) (3² – 3 x 2 + 2²)
= 5 x (9 – 6 + 4)
= 5 x 7 = 35
∴ L.H.S = R.H.S

ii) x³ – y³ = (x – y) (x² + xy + y²)
Solution:
Given that x³ – y³ = (x – y) (x² + xy + y²)
L.H.S = x³ – y³
R.H.S = (x – y) (x² + xy + y²)
= x (x² + xy + y²) – y (x² + xy + y²)
= x³ + x²y + xy² – x²y – xy² – y³
= x³ – y³= L.H.S

L.H.S = 3³ – 2³ = 27 – 8 = 19
R.H.S = (3 – 2) (3² + 3 x 2 + 2²)
= 1 x (9 + 6 + 4)
= 1 x 19 = 19
∴ L.H.S = R.H.S
We can call the above two expressions as identities

Question 10.
Factorise by using the above results (identities).
i) 27a³ + 64b³
Solution:
27a³+ 64b³ = (3a)³ + (4b)³
= (3a + 4b) {(3a)² – (3a) (4b) + (4b)²}
= (3a + 4b) (9a² – 12ab + 16b²)

ii) 343y³ – 1000
Solution:
343y³ – 1000 = (7y)³ – (10)³
= (7y – 10) [(7y)² + (7y) (10) + (10)²]
= (7y – 10) (49y² + 70y + 100)

Question 11.
Factorise 27x³ + y³ + z³ – 9xyz using identity.
Solution:
Given 27x³ + y³ + z³ – 9xyz
= (3x)³ + (y)³ + (z)³ – 3 (3x) (y) (z)
= (3x + y + z)
[(3x)² + y² + z² – (3x) (y) – (y) (z) – (z) (3x)]
[ ∵ (x³ + y³ + z³ – 3xyz = (x + y + z) (x² + y² + z²– xy – yz – zx)
= (3x + y + z) (9x² + y² + z² – 3xy – yz – 3xz)

Question 12.
Verify that x³+ y³ + z³ – 3xyz = 1/2 (x + y + z) [(x – y)² + (y – z)² + (z – x)² ]
(OR)
Verify that
p³ + q³ + r³ – 3pqr = 1/2 (p + q + r)
[(p – q)² + (q – r)² + (r – p)²]
Solution:
Given x³+ y³ + z³ – 3xyz = 1/2 (x + y + z) [(x – y)² + (y – z)² + (z – x)² ]
R-H.S = 1/2 (x + y + z) [(x – y)² + (y – z)²+ (z – x)²]
= 1/2 (x + y + z) [x² + y² – 2xy + y² + z² – 2yz + z² + x² – 2xz]
= 1/2 (x + y + z) [2x² + 2y² + 2z² – 2xy – 2yz – 2zx]
= 1/2 (x + y + z) (2) [x² + y² + z² – xy – yz – zx]
= (x + y + z) (x² + y² + z² – xy – yz – zx)
= L.H.S
Hence proved.

Question 13.
If x + y + z = 0, show that x³ + y³ + z³ = 3xyz
Solution:
Given x + y + z = 0
To prove x³ + y³ + z³ = 3xyz
We have an identity
(x + y + z) (x² + y² + z² – xy – yz – zx)
= x³ + y³ + z³ – 3xyz
Substituting x + y + z = 0in the above equation, we get
0 x (x² + y² + z² -xy-yz-zx)
= x³ + y³ + z³ – 3xyz
⇒ x³ + y³ + z³ – 3xyz = 0
⇒ x³ + y³ + z³ = 3xyz

Question 14.
Without actual calculating the cubes, find the value of each of the following.
i) (- 10)³ + 7³ + 3³
Solution:
Given (-10)³ + 7³ + 3³
Sum of the bases = -10 + 7 + 3 = = 0
∴ (- 10)³ + 7³ + 3³
= 3 (- 10) x (7) x 3
= -630
[ ∵ x + y + z = 0 then x³ + y³ + z³ = 3xyz]

ii) (28)³ + (- 15)³ + (- 13)³
Solution:
Given (28)³ + (- 15)³+ (- 13)³
Sum of the bases = 28 + (- 15) + (- 13) = 0
∴ (28)³ + (- 15)³ + (- 13)³
= 3 x 28 x (- 15) x (- 13)
= 16380

iii) \(\left(\frac{1}{2}\right)^{3}+\left(\frac{1}{3}\right)^{3}-\left(\frac{5}{6}\right)^{3}\) read it as \(\left(\frac{1}{2}\right)^{3}+\left(\frac{1}{3}\right)^{3}+\left(\frac{-5}{6}\right)^{3}\)
Solution:

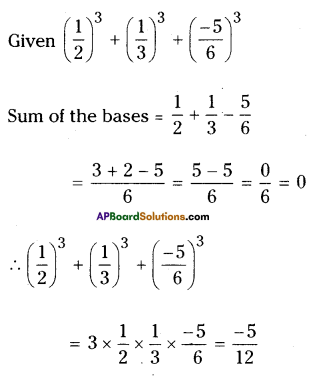
iv) (0.2)³ – (0.3)³ + (0.1)³
Solution:
Given that (0.2)³ – (0.3)³ + (0.1)³
= (0.2)³ + (- 0.3)³ + (0.1)³
Sum of the bases = 0.2 – 0.3 + 0.1 = 0
∴ (0.2)³ + (-0.3)³ + (0.1)³
= 3 x (0.2) (- 0.3) (0.1)
= -0.018

Question 15.
Give possible expressions for the length and breadth of the rectangle whose area is given by
i) 4a² + 4a – 3
Given that area = 4a² + 4a – 3
= 4a² + 6a – 2a – 3
= 2a (2a + 3) – 1 (2a + 3)
= (2a – 1) (2a + 3)
∴ Length = (2a + 3); breadth = (2a – 1).

ii) 25a² – 35a + 12
Solution:
Given that area = 25a² – 35a +12
= 25a² – 20a – 15a + 12
= 5a (5a – 4) – 3 (5a – 4)
= (5a – 4) (5a – 3)
∴ (5a – 4) (5a – 3) are the length and breadth.

Question 16.
What are the possible polynomial expressions for the dimensions of the cuboids whose volumes are given below ?
i) 3x³ – 12x
Solution:
Volume = 3x³ – 12x
= 3x (x² – 4)
= 3x (x + 2) (x – 2) are the dimensions.

ii) 12y² + 8y – 20
Solution:
Given that volume = 12y² + 8y – 20
= 4 (3y² + 2y – 5)
= 4 [3y² + 5y – 3y – 5]
= 4 [y (3y + 5) – 1 (3y + 5)]
= 4 (3y + 5) (y – 1)
Hence 4, (3y + 5) and (y – 1) are the dimensions.

Question 17.
Show that if 2 (a² + b² ) = (a + b)² then a = b
Solution:
Given that 2 (a² + b² ) = (a + b)²
To prove a = b
As 2 (a² + b² ) = (a + b)²
We have
2a² + 2b² = a² + 2ab + b²
2a² – a² + 2b² – b² = 2ab
a² + b² = 2ab
This is possible only when a = b
∴ a = b

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 2 Polynomials and Factorisation Ex 2.4 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 2nd Lesson Polynomials and Factorisation Exercise 2.4

Question 1.
Determine which of the following polynomials has (x + 1) as a factor.
i) x³ – x² – x + 1
Solution:
f(- 1) = (- 1)³ – (- 1)² – (- 1) + 1
= -1 – 1 + 1 + 1 = 0
∴ (x + 1) is a factor.

ii) x⁴ -x³ +x² – x + 1
Solution:
f(- 1) = (- 1)⁴ – (- 1)³ + (- 1)² – (- 1) + 1
= 1 + 1 + 1 + 1 + 1= 5
∴ (x + 1) is not a factor.

iii) x⁴ + 2x³ + 2x² + x + 1
Solution:
f(- 1) = (-1)⁴ + 2 (- 1)³ + 2 (- 1)² + (-1) + 1
= 1 – 2 + 2 – 1 + 1 = 1
∴ (x + 1) is not a factor.

iv) x³ – x² – (3 – √3)x + √3
Solution:
f(- 1) = (- 1)³ – (- 1)² – (3 – √3)(-1) + √3
= – 1 – 1 + 3 – √3 + √3 = 1
∴ (x + 1) is not a factor.

Question 2.
Use the factor theorem to determine whether g(x) is a factor of f(x) in each of the following cases:
i) f(x) = 5x³ + x² – 5x – 1; g(x) = x + 1
[Factor theorem : If f(x) is a polynomial; f(a) = 0 then (x – a) is a factor of f(x); a ∈ R]
Solution:
g(x) = x+ 1 = x- a say
∴ a = – 1
f(a) = f(- 1) = 5 (- 1)³ + (- 1)² – 5 (- 1) – 1
= -5 + 1 + 5 – 1 = 0
∴ x + 1 is a factor of f(x).

ii) f(x) = x³ + 3x² + 3x + 1; g(x) = x + 1
Solution:
g(x) = x + 1 = x – a
∴ a = – 1
f(a) = f(- 1) = (- 1)³ + 3 (- 1)² + 3(-1) + 1
= -1 + 3 – 3 + 1 =0
∴ f(x) is a factor of g(x).

iii) f(x) = x³ – 4x² + x + 6;
g(x) = x – 2
Solution:
g(x) = x- 2 = x- a
∴ a = 2
f(a) = f(2) = 2³ – 4(2)² + 2 + 6
= 8 – 16 + 2 + 6 = 0
∴ g(x) is a factor of f(x).

iv) f(x) = 3x³+ x² – 20x +12; g(x) = 3x – 2
Solution:
g(x) = 3x – 2 = \(x-\frac{2}{3}\) = x – a
∴ a = 2/3

v) f(x) = 4x³+ 20x²+ 33x + 18; g(x) = 2x + 3
Solution:
g(x) = 2x + 3 = x + \(\frac{3}{2}=\) = x – a
∴ a = -3/2

∴ g(x) is a factor of f(x).

Question 3.
Show that (x – 2), (x + 3) and (x – 4) are factors of x³ – 3x² – 10x + 24.
Solution:
Given f(x) = x³ – 3x² – 10x + 24
To check whether (x – 2), (x + 3) and (x – 4) are factors of f(x), let f(2), f(- 3) and f(4)
f(2) = 2³ – 3(2)² – 10(2) + 24
= 8- 12-20 + 24 = 0
∴ (x – 2) is a factor of f(x).

f(- 3) = (- 3)³ – 3(- 3)²– 10(- 3) + 24
= – 27 – 27 + 30 + 24 = 0
∴ (x + 3) is a factor of f(x).

f(4) = (4)³ – 3 (4)² – 10 (4) + 24
= 64 – 48 – 40 + 24
= 88 – 88
= 0
∴ (x – 4) is a factor of f(x).

Question 4.
Show that (x + 4), (x – 3) and (x – 7) are factors of x³ – 6x² – 19x + 84.
Solution:
Let f(x) = x³ – 6x² – 19x + 84
To verify whether (x + 4), (x – 3) and (x – 7) are factors of f(x) we use factor theorem.

Let f(- 4), f(3) and f(7)
f(- 4) = (- 4)³ – 6 (- 4)² – 19 (- 4) + 84
= -64 – 96 + 76 + 84
= 0 .
∴ (x + 4) is a factor of f(x).

f(3) = 3³ – 6(3)² – 19(3) + 84
= 27 – 54 – 57 + 84
= 0
∴ (x – 3) is a factor of f(x).

f(7) = 7³ – 6(7)² – 19(7) + 84
= 343 – 294 – 133 + 84
= 427 – 427
= 0
∴ (x – 7) is a factor of f(x).

Question 5.
If both (x – 2) and \(\left(x-\frac{1}{2}\right)\) of px² + 5x + r, show that p = r.
Solution:
Let f(x) = px²+ 5x + r
As (x – 2) and \(\left(x-\frac{1}{2}\right)\) are factor of f(x), we have f(2) = 0 and f(1/2) = 0
∴ f(2) = p(2)² + 5(2) + r
= 4p + 10 + r = 0
= 4p + r
= – 10 ………………(1)

⇒ p + 10 + 4r = 0
⇒ p + 4r = – 10 ………………. (2)
From (1) and (2);
4p + r = p + 4r
4p – p = 4r – r
3p = 3r
∴ P = r

Question 6.
If (x² – 1) is a factor of ax⁴ + bx³ + cx² + dx + e, show that a + c + e = b + d = 0.
Solution:
Let f(x) = ax⁴ + bx³ + cx² + dx + e
As (x – 1) is a factor of f(x) we have
x² – 1 = (x + 1) (x – 1) hence f(1) = 0 and f(-1) = 0
f(1) = a + b + c + d + e = 0 ……………. (1)
and f(-1) = a- b + c- d + e = 0
⇒ a + c + e = b + d
Substitute this value in equation (1)
a + c + e + b + d=0
b + d + b + d=0
2 (b + d) = 0
⇒ b + d = 0
∴ a + c + e = b + d = 0

Question 7.
Factorise
i) x³ – 2x² – x + 2
Solution:
Let f(x) = x³ – 2x² – x + 2
By trial, we find f(l) = 1³ – 2(1)² – 1 + 2
= 1 – 2 – 1 + 2
= 0 .
∴ (x – 1) is a factor of f(x).
[by factor theorem]
Now dividing f(x) by (x – 1).

f(x) = (x – 1) (x² – x – 2)
= (x – 1) [x² – 2x + x- 2]
= (x – 1) [x (x – 2) + 1 (x – 2)]
= (x – 1) (x – 2) (x + 1)

ii) x³ – 3x² – 9x – 5
Solution:
Let f(x) = x³ – 3x² – 9x – 5By trial,
f(- 1) = (- 1)³ – 3(- 1)² – 9(- 1) – 5
=-1 – 3 + 9 – 5
=0
∴ (x + 1) is a factor of f(x).
[ ∵ by factor theorem]
Now dividing f(x) by (x + 1).

f(x)=(x + 1)(x² – 4x – 5)
But x²– 4x – 5 = x² – 5x + x – 5
= x (x – 5) + 1 (x – 5)
=(x – 5)(x + 1)
∴ f(x)=(x + 1)(x + 1)(x – 5)

iii) x³ + 13x² + 32x + 20
Solution:
Let f(x) = x³ + 13x² + 32x + 20
Let f(- 1)
= (- 1)³ + 13 (- 1)² + 32 (- 1) + 20
= – 1 + 13 – 32 + 20 = 33 – 33 = 0
∴ (x + 1) is a factor of f(x).
[ ∵ by factor theorem] Now dividing f(x) by (x + 1).

iv) y³ + y² – y – 1
Let f(y) = y³ + y² – y – 1
f(1) = 1³+ 1²– 1 – 1 = 0
(y – 1) is a factor of f(y).
Now dividing f(y) by (y – 1).

∴ f(x) = (x + 1)(x² + 12x + 20)
But (x² + 12x + 20) = x²+ 10x + 2x + 20
=x(x + 10)+2(x + 10)
=(x + 10)(x + 2)
∴f(x) = (x + 1)(x + 2)(x + 10)

Question 8.
If ax² + bx + c and bx² + ax + c have a common factor x + 1 then show that c = 0 and a = b.
Solution:
Let f(x) = ax² + bx + c and g(x) = bx² + ax + c given that (x + 1) is a common factor for both f(x) and g(x).
∴ f(-1) = g(- 1)
⇒a(- 1)² + b(- 1) + c
= b(- 1)² + a (- 1) + c
⇒ a – b + c = b – a + c
⇒ a + a = b + b
⇒ 2a = 2b
⇒ a = b
Also f(- 1) = a – b + c = 0
⇒ b – b + c = 0
⇒ c = 0

Question 9.
If x² – x – 6 and x² + 3x – 18 have a common factor x – a then find the value of a.
Solution:
Let f(x) = x² – x – 6 and
g(x) = x² + 3x – 18
Given that (x – a) is a factor of both f(x) and g(x).
f(a) = g(a) = 0
⇒ a² – a – 6 = a² + 3a – 18
⇒ – 4a = – 18 + 6
⇒ – 4a = – 12
∴ a = 3

Question 10.
If (y – 3) is a factor of y³– 2y²– 9y + 18, then find the other two factors.
Solution:
Let f(y) = y³– 2y² – 9y + 18
Given that (y – 3) is a factor of f(y).
Dividing f(y) by (y – 3)

∴ f(y) = (y – 3) (y + y – 6)
But y² + y – 6
= y² + 3y – 2y – 6
= y (y + 3) – 2 (y + 3)
= (y + 3) (y – 2)
∴ f(y) = (y – 2)(y – 3)(y + 3)
The other two factors are (y – 2) and (y + 3).

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 2 Polynomials and Factorisation Ex 2.3 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 2nd Lesson Polynomials and Factorisation Exercise 2.3

Question 1.
Find the remainder when
x³ + 3x² + 3x + 1 is divided by the following Linear polynomials i) x + 1 Each
Solution:
Let f(x) = x³ + 3x² + 3x + 1
By remainder theorem, the remainder is f (- 1)
f (- 1) = (- 1)³ + 3(- 1)² + 3(- 1) + 1
= – 1 + 3 – 3 + 1 = 0

ii) \(x-\frac{1}{2}\)
f(x) = x³ + 3x² + 3x + 1
By remainder theorem, the remainder is \(\mathrm{f}\left(\frac{1}{2}\right)\)

iii) x
Solution:
f(x) = x³ + 3x² + 3x + 1
The remainder is f(0)
∴ f(0) = 0³ + 3(0)² + 3(0) + 1 = 1

iv) x + π
Solution:
f(x) = x³ + 3x² + 3x + 1
By remainder theorem, the remainder is f(- π)
f(- π) = (- π)³ + 3(-π)² + 3 (-π) + 1 .
= – π³ + 3π² – 3π + 1

v) 5 + 2x
f(x) = x³ + 3x² + 3x + 1
The remainder is \(\mathrm{f}\left(\frac{-5}{2}\right)\)

Question 2.
Find the remainder when x³ – px² + 6x – p is divided by x – p.
Solution:
Let f(x) = x³ – px² + 6x – p
(x – a) = x – p)
By Remainder theorem, the remainder is f(p)
∴ f(P) = P³ – P(P)² + 6p – p
= p³ – p³ + 5p = 5p

Question 3.
Find the remainder when 2x² – 3x + 5 is divided by 2x – 3. Does it exactly divide the polynomial ? State reason.
Solution:
Let f(x) = 2x² – 3x + 5 and
x – a = 2x – 3 = x – \(\frac{3}{2}\)
By Remainder theorem f(x) when divided by (x – \(\frac{3}{2}\) ) leaves a remainder \(\mathrm{f}\left(\frac{3}{2}\right)\)

As the remainder is 5 we say that (2x – 3) is not a factor of f(x).

Question 4.
Find the remainder when 9x³ – 3x² + x – 5 is divided by x – \(\frac{2}{3}\)
Solution:
Let f(x) = 9x³ – 3x² + x – 5
x-a = x – \(\frac{2}{3}\)
Remainder theorem the remainder is \(\mathrm{f}\left(\frac{2}{3}\right)\)

Question 5.
If the polynomials 2x³ + ax² + 3x – 5 and x³ + x² – 4x + a leave the same remainder, when divided by x – 2, find the value of a.
Solution:
Let f(x) = 2x³ + ax² + 3x – 5
g(x) = x³ + x² – 4x + a
Given that f(x) and g(x) divided x – 2
give same remainder.
i e., f(2) = g(2)
By Remainder theorem.
But f(2) = 2(2)³ + a(2)² + 3(2) – 5
= 2 x 8 + 4a + 6 – 5
= 17 +4a
g(2) = 2³ + 2² – 4(2) + a .
= 8 + 4 – 8 + a = 4 + a
i.e., 4 + a = 17 + 4a
∴ a – 4a = 17 – 4
– 3a = 13
a = -13/3

Question 6.
If the polynomials x³ + ax² + 5 and x³ – 2x² + a are divided by (x + 2) leave the same remainder, find the value of a.
Solution:
Let f(x) = x³ + ax² + 5
g(x) = x³ – 2x² + a
Given that when f(x) and g(x) divided by (x + 2) leaves the same remainder.
i.e.,f(-2) = g(-2)
By Remainder theorem
f(- 2) = (- 2)³ + a(- 2)² + 5
= -8 + 4a + 5 = 4a – 3
g(- 2) = (- 2)³ – 2(- 2)² + a
= -8 – 8 + a = a – 16
By problem,
4a – 3 = a – 16
4a – a = – 16 + 3
⇒ 3a = – 13 ⇒ a = -13/3

Question 7.
Find the remainder when f(x) = x⁴ – 3x² + 4 is divided by g(x) = x – 2 and verify the result by actual division.
Solution:
Given f(x) = x⁴ – 3x² + 4
g(x) = x – 2
The remainder when f(x) is divided by g(x) is f(2).
f(2) = 2⁴ – 3(2)² + 4
= 16 – 12 + 4
= 8
Actual division

∴ The remainder either by Remainder theorem or by actual division is the same.

Question 8.
Find the remainder when p(x) = x³ – 6x² + 14x – 3 is divided by g(x) = 1 – 2x and verify the result by long division method.
Solution:
Given p(x) = x³ – 6x² + 14x – 3
g(x) = 1 – 2x
By Remainder theorem when p(x) is divided by g(x) is p(1/2).

Question 9.
When a polynomial 2x³ + 3x² + ax + b is divided by (x – 2) leaves remainder 2, and (x + 2) leaves remainder – 2. Find a and b.
Solution:Let f(x) = 2x³ + 3x² + ax + b
The remainder when f(x) is divided by (x – 2) is 2.
i.e., f(2) = 2
⇒ 2(2)³ + 3(2)²+ a(2) + b = 2
⇒ 16 + 12 + 2a +b = 2
⇒ 2a + b = – 26 …………………..(1)

Also the remainder when f(x) is divided by (x + 2) is – 2.
i.e., f(- 2) = – 2
⇒ 2(- 2)³ + 3(- 2)² + a (- 2) + b = – 2
⇒ -16 + 12 – 2a + b = – 2
– 2a + b = 2 ………………..(2)
Solving (1) and (2),

b = – 12
and 2a – 12 = – 26
2a = -26+ 12
a = -14/2 = -7,
a = -7, b = – 12

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 2 Polynomials and Factorisation Ex 2.2 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 2nd Lesson Polynomials and Factorisation Exercise 2.2

Question 1.
Find the value of the polynomial 4x² – 5x + 3, when
(i) x = 0
Solution:
The value at x = 0 is
4(0)² – 5(0) + 3
= 3

(ii) x = – 1
Solution:
The value at x = – 1 is
4 (- 1)² – 5 (- 1) + 3
= 4 + 5 + 3
= 12

iii) x = 2
Solution:
The value at x = 2 is
4(2)² – 5(2) + 3
= 16 -10 + 3
= 9

iv) x = \(\frac{1}{2}\)
Solution:

Question 2.
Find p(0), p(1) and p(2) for each of the following polynomials.
i) p(x) = x² – x + 1
Solution:
p(0) = 0² – 0 + 1 = 1
p(1) = 1² – 1 + 1 = 1
p(2) = 2² – 2 + 1 = 3

ii) P(y) = 2 + y + 2y² – y³
Solution:
p(0) = 2 + 0 + 2(0)² – 0³ = 2
p(1) = 2+ 1 + 2(1)² – 1³ = 4
p(2) = 2 + 2 + 2(2)² -2³ = 4 + 8- 8 = 4

iii) P(z) = z³
Solution:
p(0) = 0³ = 0
p(1) = 1³ = 1
p(2) = 2³ = 8

iv) p(t) = (t – 1)(t + 1) = t² – 1
Solution:
p(0) = (0 – 1) (0 + 1) = – 1
p(1) = t² – 1 = 1² – 1 = 0
p(2) = 2² – 1 = 4 – 1 = 3

v) p(x) = x² – 3x + 2
Solution:
p(0) = 0² – 3(0) + 2 = 2
p(1) = 1² – 3(1) + 2 = 1 – 3 + 2 = 0
p(2) = 2² – 3(2) + 2 = 4- 6 + 2 = 0

Question 3.
Verify whether the values of x given in each case are the zeroes of the polynomial or not ?
i) p(x) = 2x + 1; x = \(\frac{-1}{2}\)
Solution:
The value of p(x) at x = \(\frac{-1}{2}\) is
\(\mathrm{p}\left(\frac{-1}{2}\right)=2\left(\frac{-1}{2}\right)+1\)
= -1 + 1 = 0
∴ x = \(\frac{-1}{2}\) is a zero of p(x).

(ii) p(x) = 5x – π ; x = \(\frac{-3}{2}\)
Solution:
The value of p(x) at x = \(\frac{-3}{2}\) is
\(\mathrm{p}\left(\frac{-3}{2}\right)=5\left(\frac{-3}{2}\right)-\pi=\frac{-15}{2}-\pi \neq 0\)
∴ x = \(\frac{-3}{2}\) is not a zero of p(x).

iii) p(x) = x² – 1; x = ±1
Solution:
The value of p(x) at x = 1 and – 1 is
p(1) = 1² – 1 = 0
p(-1) = (-1)² -1 = 0
∴ x = ±1 is a zero of p(x).

iv) p(x) = (x – 1) (x + 2); x = – 1, – 2
Solution:
The value of p(x) at x = – 1 is
p(-1) = (-1 – 1) (-1 + 2)
=-2 x 1 =-2 ≠ 0
Hence x = – 1 is not a zero of p(x).
And the value of p(x) at x = – 2 is
p (- 2) = (- 2 – 1) (- 2 + 2) = – 3 x 0 = 0
Hence, x = – 2 is a zero of p(x).

v) p(y) = y²; y = o
Solution:
The value of p(y) at y = 0 is p(0) = 0² = 0
Hence y = 0 is a zero of p(y).

vi) p(x) = ax + b ; x = \(\frac{-\mathbf{b}}{\mathbf{a}}\)
Solution:
The value of p(x) at x = \(\frac{-\mathbf{b}}{\mathbf{a}}\) is
\(\mathrm{p}\left(\frac{-\mathrm{b}}{\mathrm{a}}\right)=\mathrm{a}\left(\frac{-\mathrm{b}}{\mathrm{a}}\right)+\mathrm{b}\)
= -b + b = 0
∴ x = \(\frac{-\mathbf{b}}{\mathbf{a}}\) is a zero of p(x).

vii) f(x) = 3x² – 1; x = \(\frac{-1}{\sqrt{3}}, \frac{2}{\sqrt{3}}\)
Solution:

viii) f(x) = 2x – 1; x = \(\frac{1}{2} ;-\frac{1}{2}\)
Solution:

Question 4.
Find the zero of the polynomial in each of the following cases.
i) f(x) = x + 2
Solution:
x + 2 = 0
x = – 2

ii) f(x) = x – 2
Solution:
x – 2 = 0
x = 2

iii) f(x) = 2x + 3
Solution:
2x + 3 = 0
2x = – 3
x = \(\frac{-3}{2}\)

iv) f(x) = 2x – 3
Solution:
2x – 3 = 0
2x = 3
x = \(\frac{3}{2}\)

v) f(x) = x²
Solution:
x² = 0
x = 0

vi) f(x) = px, p ≠ 0
Solutin:
px = 0
x = 0

vii) f(x) = px + q; p ≠ 0; p, q are real numbers.
Solution:
px + q = 0
px = -q
x = \(\frac{-\mathrm{q}}{\mathrm{p}}\)

Question 5.
If 2 is a zero of the polynomial p(x) = 2x² – 3x + 7a, find the value of
a.
Solution:
Given that 2 is a zero of p(x) = 2x² – 3x + 7a
(i.e.) p(2) = 0
⇒ 2(2)² – 3(2) + 7a = 0
⇒ 8 – 6 + 7a = 0
⇒ 2 + 7a = 0
⇒ 7a = – 2
⇒ a = \(\frac{-2}{7}\)

Question 6.
If 0 and 1 are the zeroes of the polynomial f(x) = 2x³ – 3x² + ax + b, find the values of a and b.
Solution:
Given that f(0) = 0; f(1) = 0 and
f(x) = 2x³ – 3x² + ax + b
∴ f(0) = 2(0)³ – 3(0)² + a(0) + b
⇒ 0 = b
Also f(1) = 0
⇒ 2(1)³ – 3(1)² + a(1) + 0 = 0
⇒ 2 – 3 + a = 0 .
⇒ a = 1
Hence a = 1; b = 0

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 2 Polynomials and Factorisation Ex 2.1 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 2nd Lesson Polynomials and Factorisation Exercise 2.1

Question 1.
Find the degree of each of the polynomials given below,
i) x⁵ – x⁴ + 3
Solution:
Degree is 5.

ii) x² + x – 5
Solution:
Degree is 2.

iii) 5
Solution:
Degree is 0.

iv) 3x⁶ + 6y³ – 7
Solution:
Degree is 6.

v) 4 – y²
Solution:
Degree is 2.

vi) 5t – √3
Solution:
Degree is 1.

Question 2.
Which of the following expressions are polynomials in one variable and which are not ? Give reasons for your answer.
i) 3x² – 2x + 5
Solution:
Given expression is a polynomial in one variable.

ii) x² + √2
Solution:
Given expression is a polynomial in one variable.

iii) p² – 3p + q
Solution:
Given expression is not a polynomial in one variable. It involves two variables p and q.

iv) y + \(\frac{2}{\mathbf{y}}\)
Solution:
Given expression is not a polynomial. Since the second term contains the variable in its denominator.

v) \(5 \sqrt{x}+x \sqrt{5}\)
Solution:
Given expression is not a polynomial. Since the first term’s exponent is not an integer.

vi) x¹⁰⁰ + y¹⁰⁰
Solution:
Given expression has two variables. So it is not a polynomial in one variable.

Question 3.
Write the coefficient of x³ in each of the following.
i) x³ + x + 1
ii) 2 – x³+ x²
iii) \(\sqrt{2} x^{3}+5\)
iv) 2x³ + 5
v) \(\frac{\pi}{2} x^{3}+x\)
vi) \(-\frac{2}{3} x^{3}\)
vii) 2x² + 5
viii) 4
Solution:
i) x³ + x + 1 : co-efficient of x³ is 1.
ii) 2 – x³+ x² : co-efficient of x³ is – 1.
iii) \(\sqrt{2} x^{3}+5\) co-efficient of x³ is √2
iv) 2x³ + 5 : co-efficient of x³ is 2.
v) \(\frac{\pi}{2} x^{3}+x\) co-efficient of x³ is \(\frac{\pi}{2}\)
vi) \(-\frac{2}{3} x^{3}\) co-efficient of x³ is \(-\frac{2}{3}\)
vii) 2x² + 5 : co-efficient of x³ is ‘0’.
viii) 4 : co-efficient of x³ is ‘0’.

Question 4.
Classify the following as linear, quadratic and cubic polynomials.
i) 5x²+ x – 7 : degree 2 hence quadratic polynomial.
ii) x – x³ , : degree 3 hence cubic polynomial.
iii) x² + x + 4 : degree 2 hence quadratic polynomial.
iv) x – 1 : degree 1 hence linear polynomial.
v) 3p : degree 1 hence linear polynomial.
vi) πr² : degree 2 hence quadratic polynomial.

Question 5.
Write whether the following statements are True or False. Justify your answer.
i) A binomial can have at the most two terms
ii) Every polynomial is a binomial
iii) A binomial may have degree 3
iv) Degree of zero polynomial is zero
v) The degree of x² + 2xy + y² is 2
vi) πr² is monomial
Solution :
i) A binomial can have at the most two terms -True
ii) Every polynomial is a binomial – False
[∵ A polynomial can have more than two terms]
iii) A binomial may have degree 3 – True
iv) Degree of zero polynomial is zero – False
v) The degree of x² + 2xy + y² is 2 – True
vi) πr² is monomial – True

Question 6.
Give one example each of a monomial and trinomial of degree 10.
Solution :
– 7x¹⁰ is a monomial of degree 10.
3x²y⁸ + 7xy – 8 is a trinomial of degree 10.

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 1 Real Numbers Ex 1.3 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 1st Lesson Real Numbers Exercise 1.4

Question 1.
Simple the following expressions.
i) (5 + √7) (2 + √5)
Solution:
(5 + √7) (2 + √5)
= 10 + 5√5 + 2√7 + √35

ii) (5 + √5) (5 – √5)
Solution:
(5 + √5) (5 – √5)
= 5² + (√5)²
= 25 – 5 = 20

(iii) (√3 + √7)²
Solution:
(√3 + √7)²
= (√3)² + (√7)² + 2(√3)(√7)
= 3 + 7 + 2√21
= 10 + 2√21

iv) (√11 – √7) (√11 + √7)
= (√11)² – (√7)²
= 11 – 7 = 4

Question 2.
Classify the following numbers as rational or irrational.
i) 5 – √3
ii) √3 + √2
iii) (√2 – 2)²
iv) \(\frac{2 \sqrt{7}}{7 \sqrt{7}}\)
v) 2π
vii) (2 +√2) (2 – √2)
Solution:
i) 5 – √3 – irrational
ii) √3 + √2 – irrational
iii) (√2 – 2)² – irrational
iv) \(\frac{2 \sqrt{7}}{7 \sqrt{7}}\) – rational
v) 2π – Transcendental number. (not irrational)
vi) \(\frac{1}{\sqrt{3}}\)– irrational
vii) (2 +√2) (2 – √2) – rational

Question 3.
In the following equations, find whether variables x, y, z etc., represents rational or irrational numbers.
i) x² = 7
ii) y² = 16
iii) z² = 0.02
iv) u² = \(\frac{17}{4}\)
v) w² = 27
vi) t⁴ = 256
Solution:
i) x² = 7
⇒ x = √7 is an irrational number.
ii) y² = 16 ⇒ y = 4 is a rational number.
iii) z² = 0.02 ⇒ z = \(\sqrt{0.02}\) is an irrational number.
iv) u² = \(\frac{17}{4}\) ⇒ x = \(\frac{\sqrt{17}}{2}\) is an irrational number.
v) w² = 27 ⇒ w = \(3 \sqrt{3}\) an irrational number.
vi) t⁴ = 256 ⇒ t² = \(\sqrt{256}\) = 16
⇒ t = \(\sqrt{16}\) = 4 is a rational number

Qeustion 4.
The ratio of circumference to the diameter of a circle c/d is represented by π. But we say that π is an irrational number. Why?

Question 5.
Rationalise the denominators of the following.
i) \(\frac{1}{3+\sqrt{2}}\)
Solution:

ii) \(\frac{1}{\sqrt{7}-\sqrt{6}}\)
Solution:

iii) \(\frac{1}{\sqrt{7}}\)
Solution:

iv) \(\frac{\sqrt{6}}{\sqrt{3}-\sqrt{2}}\)
Solution:

Question 6.
Simplify each of the following by rationalising the denominator.
i) \(\frac{6-4 \sqrt{2}}{6+4 \sqrt{2}}\)
Solution:

ii) \(\frac{\sqrt{7}-\sqrt{5}}{\sqrt{7}+\sqrt{5}}\)
Solution:

iii) \(\frac{1}{3 \sqrt{2}-2 \sqrt{3}}\)
Solution:

iv) \(\frac{3 \sqrt{5}-\sqrt{7}}{3 \sqrt{3}+\sqrt{2}}\)
Solution:

Question 7.
Find the value of \(\frac{\sqrt{10}-\sqrt{5}}{2 \sqrt{2}}\) upto three decimal places. (take \(\sqrt{2}\) = 1.414, \(\sqrt{3}\) = 1.732 and \(\sqrt{5}\) = 2.236).
Solution:

Question 8.
Find
i) 64^1/6
Solution:
= (2⁶)^1/6
= 6

ii) 32^1/5
Solution:
32^1/5
= (2⁵)^1/5
= 2

iii) 625^1/4
625^1/5
= (5⁴)^1/4
= 5

iv) 16^3/2
Solution:
16^3/2
= (4²)^3/2

v) 243^2/5
Solution:
243^2/5
= (3⁵)^2/5

vi) (46656)^-1/6
Solution:

Question 9.
Simplify \(\sqrt[4]{81}-8 \sqrt[3]{343}+15 \sqrt[5]{32}+\sqrt{225}\)
Solution:

Question 10.
If ‘a’ and ‘b’ are rational numbers, find the values of a and b in each of the following equations.
i) \(\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}=\mathbf{a}+\mathbf{b} \sqrt{6}\)
Solution:
Given that \(\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}=\mathbf{a}+\mathbf{b} \sqrt{6}\)
Rationalising the denominator we get

Comparing 5 + 2√6 with a + b√6
We have a = 5 and b = 2

ii) \(\frac{\sqrt{5}+\sqrt{3}}{2 \sqrt{5}-3 \sqrt{3}}=a-b \sqrt{15}\)
Solution:
Given that \(\frac{\sqrt{5}+\sqrt{3}}{2 \sqrt{5}-3 \sqrt{3}}=a-b \sqrt{15}\)
Rationalising the denominator we get

AP Board 9th Class Maths Solutions

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 1 Real Numbers Ex 1.3 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 1st Lesson Real Numbers Exercise 1.3

Question 1.
Visualise \(2.8 \overline{74}\) on the number line, using successive magnification.
Solution:

Question 2.
Visualise \(5 . \overline{28}\) on the number line, upto 3 decimal places.
Solution:

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 1 Real Numbers Ex 1.2 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 1st Lesson Real Numbers Exercise 1.2

Question 1.
Classify the following numbers as rational or irrational.
i) \(\sqrt{27}\)
ii) \(\sqrt{441}\)
iii) 30.232342345
iv) 7.484848
v) 11.2132435465
vi) 0.3030030003
Solution:
i) \(\sqrt{27}\) – irrational number
ii) \(\sqrt{441}\) = 21 – rational
iii) 30.232342345 – irrational number
iv) 7.484848 – rational number
v) 11.2132435465 – irrational number
vi) 0.3030030003 – irrational number

Question 2.
Explain with an example how irrational numbers differ from rational numbers ?
Solution:
Irrational numbers can’t be expressed in \(\frac { p }{ q }\) form where p and q are integers and q ≠ 0.
E.g.\(\sqrt{2}, \sqrt{3} ; \sqrt{5}, \sqrt{7}\) etc.
Where as a rational can be expressed in \(\frac { p }{ q }\) form
E.g. :- -3 = \(\frac { -3 }{ 1 }\) and \(\frac { 5 }{ 4 }\) etc.

Question 3.
Find an irrational number between \(\frac { 5 }{ 7 }\) and \(\frac { 7 }{ 9 }\). How many more there may be ?
Solution :
The decimal forms of \(\frac { 5 }{ 7 }\) and \(\frac { 7 }{ 9 }\) are
\(\frac{5}{7}=0 . \overline{714285} \ldots ., \frac{7}{9}=0.7777 \ldots \ldots=0 . \overline{7}\)
∴ An irrational between \(\frac { 5 }{ 7 }\) and \(\frac { 7 }{ 9 }\) is 0.727543…………
There are infinitely many irrational numbers between \(\frac { 5 }{ 7 }\) and \(\frac { 7 }{ 9 }\).

Question 4.
Find two irrational numbers between 0.7 and 0.77.
Solution:
Two irrational numbers between 0.7 and 0.77 can take the form
0.70101100111000111…………. and 0.70200200022……………

Question 5.
Find the value of √5 uPto 3 decimal places.
Solution:

[√5 is not exactly equal to 2.2350679………….. as shown ¡n calculators]

Question 6.
Find the value of √7 upto six decimal places by long division method.
Solution:

Question 7.
Locate \(\sqrt{\mathrm{10}}\) on number line.

Step – 1 : Draw a number line.
Step – 2 : Draw a rectangle OABC at zero with measures 3 x 1. i.e., length 3 units and breadth 1 unit.
Step – 3 : Draw the diagonal OB.
Step – 4 : Draw an arc with centre ‘O’ and radius OB which cuts the number line at D.
Step – 5 : ‘D’ represents \(\sqrt{\mathrm{10}}[latex] on the number line.

Question 8.
Find atleast two irrational numbers between 2 and 3.
Solution:
An irrational number between a and b is Tab [latex]\sqrt{\mathrm{ab}}\) unless ab is a perfect square.
∴ Irrational number between 2 and 3 is √6

∴ Required irrational numbers are 6^1/2, 24^1/4

Method – II:
Irrational numbers between 2 and 3 are of the form 2.12111231234………….. and 3.13113111311113…….

Question 9.
State whether the following statements are true or false. Justify your answers.
Solution:

1. Every irrational number is a real number – True (since real numbers consist of rational numbers and irrational numbers)
2. Every rational number is a real number – True (same as above)
3. Every rational number need not be a rational number – False (since all rational numbers are real numbers).
4. \(\sqrt{n}\) is not irrational if n is a perfect square – True. (since by definition of an irrational number).
5. \(\sqrt{n}\) is irrational if n is not a perfect square – True. (same as above)
6. All real numbers are irrational – False (since real numbers consist of rational